
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Односторонние пределы
Определение 66.Правой окрестностью точки а называется любой интервал 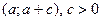 .
.
Пусть функция  определена в некоторой правой окрестности точки
определена в некоторой правой окрестности точки  .
.
Определение 67.Число 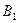 называется пределом справа функции
называется пределом справа функции  в точке
в точке  , если для любого положительного числа
, если для любого положительного числа 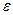 найдётся такое положительное число
найдётся такое положительное число 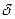 , что для всех
, что для всех  , удовлетворяющих условию
, удовлетворяющих условию 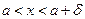 , выполняется неравенство
, выполняется неравенство  . При этом пишут:
. При этом пишут: 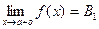 . Часто вместо
. Часто вместо  пишут
пишут 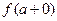 .
.
То есть 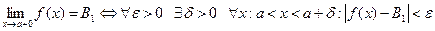 .
.
Аналогично определяется предел слева.
Определение 68.Левой окрестностью точки  называется любой интервал
называется любой интервал 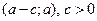 .
.
Пусть функция  определена в некоторой левой окрестности точки
определена в некоторой левой окрестности точки  .
.
Определение 69.Число 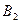 называется пределом слева функции
называется пределом слева функции  , если для любого положительного числа
, если для любого положительного числа 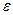 найдётся такое положительное число
найдётся такое положительное число 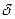 , что при всех
, что при всех  , удовлетворяющих условию
, удовлетворяющих условию 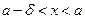 , выполняется неравенство
, выполняется неравенство  . При этом пишут:
. При этом пишут: 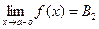 или
или 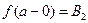 .
.
То есть 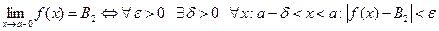 .
.
Наглядное представление об односторонних пределах дает:
Пример 74.Пусть 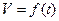 - объем 1кг
- объем 1кг 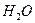 при температуре
при температуре  . Тогда
. Тогда  - объем 1кг льда при температуре
- объем 1кг льда при температуре 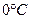 , а
, а 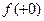 объем 1кг жидкой воды при той же температуре. Из курса физики известно, что
объем 1кг жидкой воды при той же температуре. Из курса физики известно, что  (это обстоятельство приводит, например, к тому, что при замерзании воды в водопроводных трубах они лопаются).
(это обстоятельство приводит, например, к тому, что при замерзании воды в водопроводных трубах они лопаются).
►Теорема 20.(необходимое и достаточное условие существования предела функции в точке). Для того, чтобы число 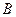 было пределом функции
было пределом функции 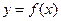 в точке, необходимо и достаточно, чтобы существовали оба односторонних предела
в точке, необходимо и достаточно, чтобы существовали оба односторонних предела 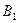 и
и 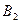 и они были равны между собой:
и они были равны между собой: 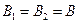 .
.
Докажите эту теорему самостоятельно.
Пример 75.Пусть  . Найдем односторонние пределы этой функции в точке
. Найдем односторонние пределы этой функции в точке 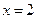 .
.
 , тогда
, тогда 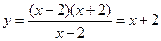 ;
; 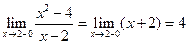 ;
;
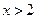 , тогда
, тогда 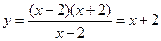 ;
; 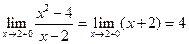 .
.
Итак, 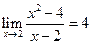 .
.
Дата добавления: 2014-11-13; просмотров: 281; Мы поможем в написании вашей работы!; Нарушение авторских прав |