Основные теоремы о пределах функций

Основные теоремы о пределах функций при аналогичны теоремам о пределах последовательностей.

►Теорема 17.Если при функции и 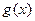имеют конечные пределы, то при существует также предел их суммы и произведения, при этом

1) ;

2) ;

3) Если , то существует предел частного и .

4) Если 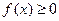, то .

Доказательство:

1) Обозначим . Тогда , , где функции и - бесконечно малы при . Значит, . По теореме о сумме бесконечно малых функций, бесконечно мала при . Следовательно, .

2) Рассуждая аналогично имеем: . По теоремам 13 и 14 о бесконечно малых функциях бесконечно мала при . Следовательно, .

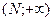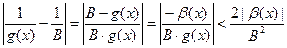3) Сначала докажем, что , где . Так как , то , где - бесконечно мала при . Тогда найдется луч , на котором , значит, . На этом луче имеем . Так как бесконечно мала при , то функция 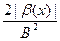бесконечно мала при и поэтому . При имеем: .

Примечание: Аналогичные свойства имеют место 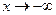при и при .

Следствие 3. Предел постоянной равен этой постоянной и постоянный множитель можно выносить за знак предела.