Основные определения. Никакие два класса делятся логические ошибки?

Никакие два класса делятся логические ошибки? Что такое Komonymia? Что такое ignoratio elenchi? Что такое qui nimium probat nihil probat? Что называется доказательством ad hominem? Что назы­вается основной ошибкой? Что такое petitio principii? Что такое idem per idem? Что называется circulus in demonstrando? Какая ошибка называется fallacia a dicto secundum quid ad dictum simpliciter? Какая ошибка называется fallacia a sensu composite ad sensum divisum? Какая ошибка называется fallacia a sensu diviso ad sensum compositum? Перечислите, какие существуют ошибки индукции, н объясните их. Какое различие между софизмами и паралогизмами?

Предел функции на бесконечности

Основные определения

Аналогично определению предела последовательности введём определение предела функции на бесконечности.

Известно, что .

Пусть функция определена в окрестности бесконечности (то есть, определена вне некоторого отрезка , где ).

Определение 56.Число 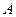называется пределом функции при , стремящемся к бесконечности, если для любого положительного числа 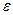найдётся такое положительное число , что для всех , удовлетворяющих условию , выполняется неравенство .

Обозначается: .

С использованием кванторов определение записывается так:

Пример 64.Доказать, что .

Доказательство:Функция определена для всех . Для любого неравенство или будет выполняться, если . Таким образом

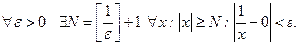
Это и означает, что .

Часто различают существование пределов функции отдельно при и .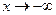

Определение 57.

Определение 58.

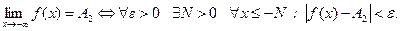
Определение 59.