Бесконечно большие функции и их связь с бесконечно малыми функциями.

По аналогии с бесконечно большими последовательностями определим бесконечно большую при функцию.

Определение 61.Функция 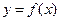, определённая на луче 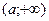, называется бесконечно большой при , если для любого сколь угодно большего числа 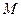, существует такое, что для всех из интервала 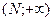выполняется неравенство .

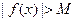Запишем это определение с помощью кванторов: .

Иногда тот факт, что – бесконечно большая при записывают так: .

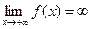Аналогично определяется бесконечно большая функция 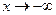при и при .

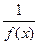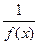►Теорема 18.Если – бесконечно малая функция при и , то – бесконечно большая при , и наоборот, если – бесконечно большая функция при , то – бесконечно малая функция при .

Доказательство:полностью аналогично доказательству для последовательностей.

Примечание: Аналогичные теоремы справедливы 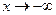при и при .

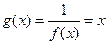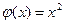Пример 69.Функция , бесконечно малая при , а функция - бесконечно большая при ; функция бесконечно большая при , тогда функция - бесконечно малая при .

Пример 70.Вычислим пределы:

1) 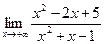. При числитель и знаменатель дроби 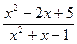бесконечно большие функции. Потому теорема о пределе частного неприменима. Но значение дроби не изменится, если числитель и знаменатель дроби разделить на 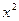(старшая степень).

= .

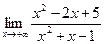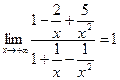2) , так как , а .

3) 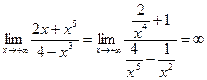, так как , а .

Легко доказать общее утверждение: