
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Горизонтальные и наклонные асимптоты
Пусть функция  определена на бесконечном интервале
определена на бесконечном интервале 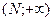 .
.
Определение 62.
 |
Прямая
 называется асимптотой графика функции
называется асимптотой графика функции  при
при  , если
, если 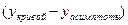 – бесконечна мала при
– бесконечна мала при  , то есть
, то есть  (см. рис. 27).
(см. рис. 27).
Аналогично для 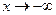 .
.
Определение 63.Прямая  называется наклонной асимптотой, если
называется наклонной асимптотой, если  . Если
. Если  , то прямая
, то прямая 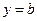 называется горизонтальной асимптотой, тогда
называется горизонтальной асимптотой, тогда  .
.
►Теорема 19.Для того, чтобы прямая  являлась асимптотой графика функции
являлась асимптотой графика функции  при
при  , необходимо и достаточно, чтобы существовали
, необходимо и достаточно, чтобы существовали  и
и  .
.
Доказательство:
1) (необходимость). Пусть прямая  – асимптота графика функции при
– асимптота графика функции при  . Это значит, что
. Это значит, что 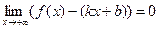 . Рассмотрим функцию
. Рассмотрим функцию 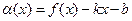 . Так как
. Так как  ,
,  , а так как
, а так как  , то
, то  .
.
2) (достаточность).
Рассмотрим функцию 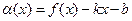 . Так как
. Так как  ,
,  , а так как
, а так как  , то
, то  . Пусть
. Пусть  ,
,  . Рассмотрим
. Рассмотрим 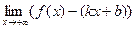 , подставляя значения
, подставляя значения  и
и 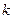 , получим, что
, получим, что 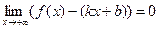 .
.
Аналогично можно показать, что если функция  определена на интервале
определена на интервале  , то для того, чтобы прямая
, то для того, чтобы прямая  являлась асимптотой функции
являлась асимптотой функции  и при
и при 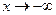 , необходимо и достаточно, чтобы существовали
, необходимо и достаточно, чтобы существовали  и
и  .
.
Пример 71.Найти наклонные асимптоты графика функции 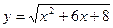 .
.


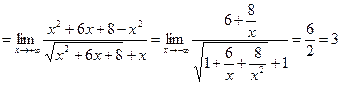 .
.
График функции 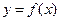 имеет асимптоту
имеет асимптоту  при
при  .
.
Найдем асимптоту графика функции при 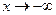 .
.


 .
.
График функции 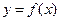 имеет асимптоту
имеет асимптоту 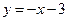 при
при 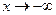 .
.
 |
Функция
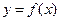 определена для
определена для 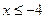 или
или  , так как
, так как 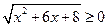 при
при 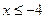 или
или  . Построим схематически график функции, состоящий из двух ветвей, вместе с наклонными асимптотами.
. Построим схематически график функции, состоящий из двух ветвей, вместе с наклонными асимптотами.
Пример 72.Найти горизонтальную асимптоту графика функции  .
.
Решение:  ; значит, прямая
; значит, прямая 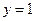 - горизонтальная асимптота графика функции
- горизонтальная асимптота графика функции  .
.
Дата добавления: 2014-11-13; просмотров: 328; Мы поможем в написании вашей работы!; Нарушение авторских прав |