
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Свойства предела функции в точке
Для функций, имеющих предел в точке, справедливы теоремы, аналогичные теоремам о пределах функций при  .
.
►Теорема 21.Если функция  имеет предел при
имеет предел при  , то этот предел единственен.
, то этот предел единственен.
►Теорема 22.Для того, чтобы функция  имела предел, равный
имела предел, равный 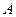 , при
, при  ,необходимо и достаточно, чтобы выполнялось соотношение:
,необходимо и достаточно, чтобы выполнялось соотношение: 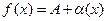 , где
, где  при
при  .
.
►Теорема 23.Если при  функции
функции  и
и 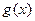 имеют пределы, то при
имеют пределы, то при  существует также предел их суммы и произведения, при этом
существует также предел их суммы и произведения, при этом
 ;
;
 ; если, кроме того,
; если, кроме того, 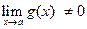 , то существует предел частного
, то существует предел частного  и
и  ; если же
; если же 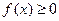 и существует
и существует  , то существует и
, то существует и  .
.
Следствие.  .
.
Вычисление пределов
Пример 76.Рассмотрим несколько упражнений, показывающих применение теорем к вычислению пределов.
1)  .
.
2)  .
.
3)  . При
. При 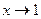 предел знаменателя равен нулю, поэтому применить теорему о пределе частного нельзя. Преобразуем дробь:
предел знаменателя равен нулю, поэтому применить теорему о пределе частного нельзя. Преобразуем дробь: 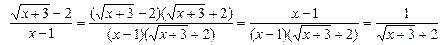 ;
;  .
.
4)  .
.
5) 
 .
.
Дата добавления: 2014-11-13; просмотров: 308; Мы поможем в написании вашей работы!; Нарушение авторских прав |