Арифметические операции над непрерывными функциями. Композиция непрерывных функций

Пусть даны две функци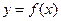и и 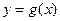, непрерывные в точке . Рассмотрим их сумму, произведение и частное. Справедливы следующие теоремы:

►Теорема 24.Сумма двух функций, непрерывных в данной точке, непрерывна в этой же точке.

►Теорема 25.Произведение двух функций, непрерывных в данной точке, непрерывно в этой же точке.

►Теорема 26.Частное двух функций, непрерывных в данной точке, непрерывно в данной точке, если значение знаменателя в данной точке не равно нулю.

Доказательство этих теорем следует из Определение 71 и соответствующих теорем о пределе суммы, произведения и частного в данной точке.

Пример 79.Докажите, что любая целая рациональная функция (многочлен) непрерывна при всех действительных .

Доказательство:из Пример 78 следует, что функция (константа) и – непрерывны для всех действительных , а из ►Теорема 24, ►Теорема 25 следует, что многочлен от переменной непрерывен при .

Пример 80.Докажите, что рациональная функция 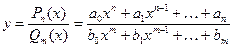непрерывна при всех , при которых .

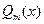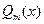Доказательство:из Пример 79 следует, что и непрерывны при всех , а из ►Теорема 26 следует, что частное и непрерывно при всех , при которых .

Рассмотрим композицию непрерывных функций.

►Теорема 27.Пусть функция непрерывна при , а функция непрерывна при , причем . Тогда сложная функция непрерывна в точке .

Доказательство:зададим . Так как функция непрерывна в точке , то найдется такое, что из неравенства следует , но функция непрерывна в точке , значит найдется такое, что из неравенства вытекает неравенство ; поскольку 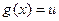, , то при 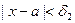имеем , а значит, .

Это и значит, что функция непрерывна в точке .

Замечание. ►Теорема 27 обобщается на любое количество композиций непрерывных функций.

Пример 81.Докажите, что функция 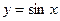непрерывна при всех действительных .

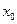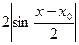
Доказательство:пусть произвольное действительное число, рассмотрим и ; преобразуем , итак, , а это означает (в силу Определение 70), что 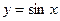непрерывна при всех действительных .

Конечно, к тому же выводу мы пришли бы, используя Определение 73. Действительно, неравенство означает, что ; значит, 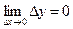и функция 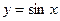– непрерывна при всех действительных .

Пример 82.Докажите, что функция непрерывна при всех действительных , удовлетворяющих условию .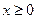

Доказательство:пусть 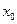произвольное положительное действительное число , рассмотрим , значит, 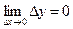, то есть функция непрерывна при всех положительных действительных . При функция непрерывна справа: .

Пример 83.Докажите, что функция непрерывна при всех действительных .

Доказательство:непрерывными являются функции ; ; . Кроме того, 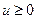при всех ; значит, непрерывна при всех действительных , как композиция непрерывных функций.