
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Свойства функций, непрерывных на отрезке
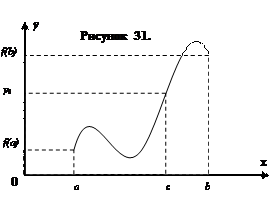 Обсуждая наглядное представление о непрерывной функции, мы говорили о ее графике, как о едином куске. Рассмотрим рис. 31.
Обсуждая наглядное представление о непрерывной функции, мы говорили о ее графике, как о едином куске. Рассмотрим рис. 31.
Если мы возьмем любую точку 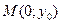 на оси ординат, лежащую между точками с ординатами
на оси ординат, лежащую между точками с ординатами 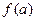 и
и 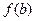 , и проведем через нее горизонтальную прямую, то эта прямая пересечет график в некоторой точке. Пусть абсцисса этой точки равна
, и проведем через нее горизонтальную прямую, то эта прямая пересечет график в некоторой точке. Пусть абсцисса этой точки равна 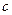 . Тогда
. Тогда  . Таким образом, для любого числа
. Таким образом, для любого числа 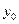 , лежащего между
, лежащего между 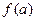 и
и 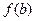 найдется такое
найдется такое 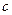 , что
, что 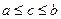 и
и  .
.
Рассмотрим рис. 32. Точка 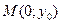 лежит между
лежит между 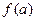 и
и 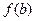 , но если провести через нее горизонтальную прямую, то эта прямая не пересечет графика функции
, но если провести через нее горизонтальную прямую, то эта прямая не пересечет графика функции 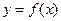 . Иными словами между точками
. Иными словами между точками  и
и  нет точки
нет точки 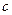 такой, что
такой, что  .
.
Рассмотрим рис. 33. Для любого 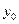 , лежащего между
, лежащего между 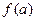 и
и 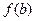 , найдется точка
, найдется точка 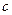 между точками
между точками  и
и  такая, что
такая, что  , тем не менее рис. 33 отличается от рисунка 31. Действительно, если вместо точек
, тем не менее рис. 33 отличается от рисунка 31. Действительно, если вместо точек  и
и  мы возьмем точки
мы возьмем точки 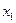 и
и 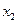 из отрезка
из отрезка 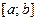 , то убедимся, что значение
, то убедимся, что значение 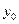 лежит между
лежит между  и
и 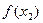 , но не существует такой точки
, но не существует такой точки 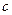 из отрезка
из отрезка 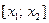 , в которой
, в которой  .
.
 Проведенные рассуждения позволяют уточнить наглядные представления о линии, состоящей из одного куска: если график функции
Проведенные рассуждения позволяют уточнить наглядные представления о линии, состоящей из одного куска: если график функции 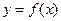 на отрезке
на отрезке 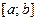 состоит из одного куска, то для любых двух точек
состоит из одного куска, то для любых двух точек 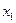 и
и 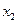 этого отрезка и любого числа
этого отрезка и любого числа 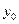 , лежащего между
, лежащего между  и
и 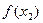 , найдется такое значение
, найдется такое значение 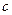 , что
, что 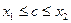 и
и  ; то есть эта функция принимает все значения, лежащие между двумя данными значениями функции.
; то есть эта функция принимает все значения, лежащие между двумя данными значениями функции.
Покажем, что этим свойством обладает график любой непрерывной функции. Верна следующая «теорема о промежуточном значении»:
►Теорема 28.(Теорема Коши). Пусть функция 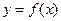 непрерывна на отрезке
непрерывна на отрезке 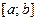 . Тогда для любых
. Тогда для любых 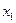 и
и 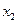 этого отрезка и любого числа
этого отрезка и любого числа 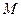 , лежащего между
, лежащего между  и
и 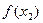 найдется
найдется 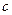 такое, что
такое, что 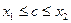 и
и  .
.
Доказательство теоремы о промежуточном значении проведем в три этапа:
I. (лемма). Пусть функция 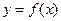 непрерывна в точке
непрерывна в точке  . Если она положительна в этой точке (
. Если она положительна в этой точке ( 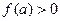 ), то существует окрестность
), то существует окрестность 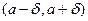 точки
точки  , в которой
, в которой 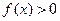 .
.
Доказательство:(леммы) так как функция 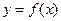 непрерывна в точке
непрерывна в точке  , то найдется такое
, то найдется такое 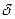 , что в окрестности
, что в окрестности 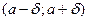 точки
точки  выполняется неравенство
выполняется неравенство 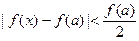 (в качестве
(в качестве 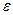 выбрано положительное число
выбрано положительное число 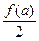 ). Тогда при
). Тогда при 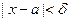 имеем:
имеем: 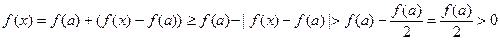 , итак,
, итак, 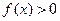 в
в 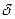 -окрестности точки
-окрестности точки  .
.
Аналогично доказывается, что если функция 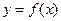 непрерывна в точке
непрерывна в точке  и отрицательна в этой точке, то она отрицательна в некоторой окрестности точки
и отрицательна в этой точке, то она отрицательна в некоторой окрестности точки  .
.
Дата добавления: 2014-11-13; просмотров: 277; Мы поможем в написании вашей работы!; Нарушение авторских прав |