III. Перейдем к доказательству теоремы о промежуточном значении

Пусть 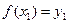, 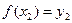и для определенности 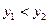, а также 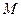– данное число, . Введем вспомогательную функцию . Эта функция непрерывна на отрезке 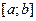, а значит, и на отрезке .

Рассмотрим ; , тогда по теореме Больцано-Вейерштрасса существует такая точка , что ; или , что и требовалось доказать.

Отметим, что при доказательстве теоремы Больцано-Вейерштрасса был сконструирован метод половинного деления (бисекции, дихотомии), широко применяемый в численных методах.

Сформулируем (без доказательства) еще несколько важных свойств функций, непрерывных на отрезке:

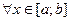
1) ограничена на , то есть (следствие из теоремы Вейерштрасса).

2) имеет на наибольшее и наименьшее значение (теорема Вейерштрасса): ; .

;

.