
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Свойство бесконечно малых функций
►Теорема 13.Если функции  и
и 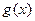 бесконечно малы при
бесконечно малы при  , то сумма
, то сумма  бесконечно мала при
бесконечно мала при  .
.
Доказательство:Так как  и
и 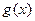 – бесконечно малые при
– бесконечно малые при  , то найдутся лучи
, то найдутся лучи  и
и 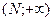 , на которых для любого
, на которых для любого  соответственно выполняются неравенства
соответственно выполняются неравенства 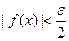 и
и 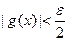 . На общей части этих лучей выполняются оба неравенства, следовательно,
. На общей части этих лучей выполняются оба неравенства, следовательно,  . Таким образом, для любого
. Таким образом, для любого  существует луч, на котором
существует луч, на котором  , значит,
, значит,  – бесконечно малая при
– бесконечно малая при  .
.
Следствие 1.Если функции  бесконечно малы при
бесконечно малы при  , то функция
, то функция  – бесконечно мала при
– бесконечно мала при  .
.
►Теорема 14.Произведение ограниченной функции на бесконечно малую – бесконечно малая функция.
Доказательство:Пусть  – ограниченная, а
– ограниченная, а 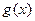 – бесконечно малая при
– бесконечно малая при  , значит,
, значит, 
 и
и

 .
.
Рассмотрим модуль произведения  для всех
для всех  , принадлежащих общей части лучей
, принадлежащих общей части лучей  и
и 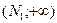 . Пусть
. Пусть  . Итак,
. Итак,  , а это значит, что
, а это значит, что  - бесконечно малая при
- бесконечно малая при 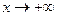 .
.
Следствие 2. Произведение конечного числа бесконечно малых – бесконечно малая при 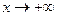 .
.
Примечание: Теорема 13 и 14 сформулированы и доказаны при 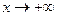 . Аналогично формулируются соответствующие теоремы при
. Аналогично формулируются соответствующие теоремы при  и
и  .
.
►Теорема 15.Для того, чтобы функция  имела при
имела при  предел, равный
предел, равный 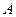 , необходимо и достаточно, чтобы выполнялось соотношение
, необходимо и достаточно, чтобы выполнялось соотношение  , где
, где  – бесконечно малая при
– бесконечно малая при  .
.
Доказательство:1) (необходимость)
Пусть  , значит,
, значит,  обозначим
обозначим  , тогда
, тогда  , где
, где  – бесконечно малая, так как
– бесконечно малая, так как  .
.
2) (достаточность)
Пусть  , где
, где  – бесконечно малая при
– бесконечно малая при  , тогда
, тогда  , но
, но  , значит,
, значит,  , таким образом,
, таким образом,  .
.
Рассмотрим несколько примеров.
Пример 66.Докажите, что 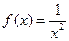 бесконечно малая при
бесконечно малая при  .
.
Доказательство:  , значит,
, значит,  - произведение функций бесконечно малых при
- произведение функций бесконечно малых при  , следовательно,
, следовательно, 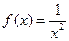 бесконечно малая при
бесконечно малая при  .
.
Докажите самостоятельно, что для любого  функция
функция  бесконечно малая при
бесконечно малая при  .
.
Пример 67.Докажите, что  , бесконечно малая при
, бесконечно малая при  .
.
Доказательство:Так как  , то при
, то при 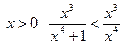 ,
,  - бесконечно малая при
- бесконечно малая при  , значит,
, значит,  , бесконечно малая при
, бесконечно малая при  .
.
Пример 68.Докажите, что  .
.
Доказательство:рассмотрим 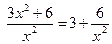 , функция
, функция  бесконечно малая при
бесконечно малая при  , бесконечно мала и функция
, бесконечно мала и функция  при
при  , значит,
, значит, 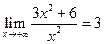 .
.
Свойства предела функции при  . Теорема о единственности предела.
. Теорема о единственности предела.
►Теорема 16.Если функция  имеет предел при
имеет предел при  , то этот предел единственен.
, то этот предел единственен.
Доказательство:Пусть  , тогда для любого
, тогда для любого  найдется такое
найдется такое  , что для всех
, что для всех  выполняются неравенства:
выполняются неравенства:  и
и  , тогда
, тогда 
Следовательно, неотрицательное число  меньше любого положительного числа
меньше любого положительного числа 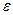 . Таким числом может быть только нуль:
. Таким числом может быть только нуль:  ,
, 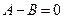 ,
, 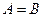 .
.
Дата добавления: 2014-11-13; просмотров: 299; Мы поможем в написании вашей работы!; Нарушение авторских прав |