Решение. Соотношение неопределенностей для координаты и импульса имеет вид:

Соотношение неопределенностей для координаты и импульса имеет вид:

Δх Δр_х ≥ 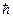, (1)

Где Δх – неопределенность координаты частицы (в данном случае электрона); Δр_х – неопределенность импульса частицы (электрона); 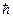= постоянная Планка.

Из соотношения неопределенностей следует, что чем точнее определяется положение частицы в пространстве, тем более неопределенным становится импульс, а следовательно, и энергия частицы. Пусть атом имеет линейные размеры l, тогда электрон атома будет находиться где-то в пределах области с неопределенностью

Δх = l /2.

Соотношение неопределенностей (1) можно записать в этом случае в виде:

(l /2) Δр_х ≥ ,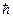

откуда

l ≥ 2 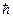/ Δр_х (2)

Физически разумная неопределенность импульса Δр_х во всяком случае не должна превышать значения самого импульса р_х , т.е. Δр_х ≤ р_х . импульс р_х связан с кинетической энергией Т соотношением р_х = mТ. Заменим Δр_х значением mТ (такая замена не увеличит l). Переходя от неравенства к равенству, получаем:

l_min = 2 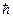/ mТ (3)

Проверим, дает ли полученная формула единицу длины. Для этого в правую часть формулы (3) вместо символов величин подставим обозначения их единиц:

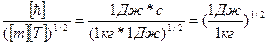1с = 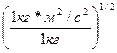1с = 1м.

найденная единица является единицей длины.

Произведем вычисления:

l_min = 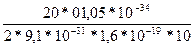м = 1,24 * 10^{-10 м = 124 нм.}

Пример 4.

Рис. 64