
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Примеры решения задач по кинематике
Пример 1.Найти по величине и направлению относительно берега скорость человека  , движущегося поперек парохода со скоростью 2 м/с, пароход движется со скоростью
, движущегося поперек парохода со скоростью 2 м/с, пароход движется со скоростью  = 8 м/с .
= 8 м/с .
Решение:

Рисунок 4 – Пример 1
Скорость  человека относительно берега является векторной суммой скоростей
человека относительно берега является векторной суммой скоростей 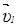 и
и  :
:
 =
= 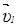 +
+  (12)
(12)
Численное значение скорости определяется:  =
=  =
=  =8,25м/с.
=8,25м/с.
Направление скорости  определяется углом a, который она составляет с направлением движения парохода:
определяется углом a, который она составляет с направлением движения парохода:  , отсюда a=14°03¢.
, отсюда a=14°03¢.
Пример 2.Камень, брошенный вертикально вверх, достигает высоты 30м. Через сколько времени он достигает этой высоты и через сколько времени он упадет обратно на землю? Какую начальную скорость ему надо сообщить?
Решение:
Движение камня вверх равнозамедленно, его ускорение а = - g, а высота поднятия
 , (13)
, (13)
где  - начальная скорость камня;
- начальная скорость камня;
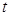 - время, в течение которого он поднимается вверх.
- время, в течение которого он поднимается вверх.
Начальная скорость определяется из условия, что скорость в высшей точке поднятия равна нулю, то есть
 ,
, 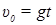 (14)
(14)
Подставляя (14) в (13), имеем
 (15)
(15)
Искомое время поднятия определяется из (15). Так как время подъема и падения равны, то камень вернется на землю через  .
.
 ,
,  .
.
Начальная скорость вычисляется по уравнению (14)

Пример 3.Точка движется по кривой согласно уравнению  .
.
Найти среднюю скорость движения точки в промежутке времени от  и
и  .
.
Решение:
Среднее значение модуля скорости точки в промежутке времени от t до  равно
равно  , где
, где  - путь, пройденный точкой за время
- путь, пройденный точкой за время  . По условию задачи y - криволинейная координата движущейся точки, а задача сводится к вычислению пути
. По условию задачи y - криволинейная координата движущейся точки, а задача сводится к вычислению пути  , пройденного точкой за промежуток времени
, пройденного точкой за промежуток времени  = t2 – t1. Предположим, что точка двигалась по кривой в течение всего промежутка времени в одном направлении, то есть
= t2 – t1. Предположим, что точка двигалась по кривой в течение всего промежутка времени в одном направлении, то есть
 =
=  = y2 - y1 ;
= y2 - y1 ;

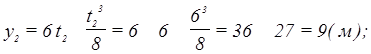
 .
.
Дата добавления: 2015-02-10; просмотров: 342; Мы поможем в написании вашей работы!; Нарушение авторских прав |