Законы динамики

Общей целью механики является установление величин, описывающих состояние тела или системы тел, а также закономерности и причины изменения состояния физической системы во времени.

Эта задача решается законами движения Ньютона. В динамике Ньютона сила является причиной изменения состояния физической системы.

Силы не являются какими-то самостоятельными сущностями, не зависимыми от материальных тел. Силы создаются материальными телами. Посредством сил материальные тела действуют друг на друга, то есть взаимодействуют.

Сила является количественной мерой интенсивности взаимодействия.

Под действием приложенной силы тела изменяют скорость движения или деформируются.

Как известно, первый закон Ньютона гласит, что тело сохраняет состояние покоя или равномерного прямолинейного движения, если оно достаточно удалено от других тел. С помощью первого закона Ньютона можно выбрать систему отсчёта, так что некоторое пробное тело, помещённое в него, удалено от других материальных тел. Если при этом, наблюдая движение пробного тела, мы обнаружим, что оно движется равномерно и прямолинейно или покоится, то система отсчёта годится для кинематических и динамических описаний движения.

Поэтому первый закон Ньютона является независимым законом, выражающим критерий пригодности системы отсчёта для рассмотрения движений. Этот закон является не только независимым, но и первым в том смысле, что только после выбора системы отсчёта можно говорить о точно определённом физическом смысле и содержании второго и третьего законов динамики.

Второй закон Ньютона даёт выражение ускорения тела под действием силы, приложенной к нему, в виде

= , (32)

где m - масса тела;

- ускорение.

Масса характеризует свойство инертности тела и для каждого тела имеет определённое значение.

Результаты экспериментов показывают, что ускорение по направлению совпадают с направлением силы. Одна и та же сила разным телам сообщает различные ускорения.

Различные силы одному и тому же телу сообщают равные ускорения. Но отношение силы к ускорению всегда равно одной и той же величине ,если учесть, что , то второй закон Ньютона примет вид

, (33)

где p - произведение массы на скорость называется импульсом тела. Сила в правой части (2) является суммой всех сил, действующих на тело. Выражения (1) и (2) отличаются только обозначениями, но имеют одно и то же физическое содержание.

Это уравнение строго применимо лишь к материальной точке. К материальному телу оно применимо, если под скоростью принимать скорость центра масс тела, а не производной точки тела.

Отношение справедливо только при малых скоростях тел.

Третий закон Ньютона говорит о том, что во взаимодействии двух тел каждое из тел действует на другое тело с одинаковой по значению, но противоположной по направлению силой.

Таким образом, источниками «действующей» и «противодействующей» сил являются различные материальные тела; различны также и тела, к которым приложены эти силы.

Каждое из взаимодействующих тел является источником «действующей» силы и объектом приложения «противодействующей» силы. Разница между «действующей» и «противодействующей» силами зависит от точки зрения наблюдателя и имеет лишь субъективный характер.

Опыт показывает, что при взаимодействии двух тел соблюдается соотношение

m₁a₁ = m₂a₂, (34)

где a₁ и a₂ - ускорение тел m₁ и m₂ , то есть

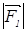= (35)

Однако закон равенства действия и противодействия выполняется в такой простой форме не всегда.

Например, при взаимодействии двух положительных зарядов учитывается и электромагнитное взаимодействие возникших полей, сила Кулона, сила Лоренца. Так как сила Лоренца перпендикулярна скорости и магнитному полю , то сила, действующая на каждый из зарядов, не совпадает по направлению, то есть не удовлетворяет закону действия и противодействия.

Результирующие силы «действия» и «противодействия» не равны друг другу и не направлены противоположно, то есть третий закон механики не выполняется, но при малых скоростях движения заряженных частиц силы магнитного происхождения много меньше электрических. А поскольку отклонение от законов обусловлено магнитными силами, то этим нарушением третьего закона можно пренебречь.

Третий закон Ньютона имеет более глубокое содержание, чем просто равенство сил действия и противодействия.

Рассмотрим взаимодействие двух тел А и В массой m₁ и m₂ (рисунок 9) и запишем уравнение движения для каждого из взаимодействующих тел:

Рисунок 9

; , (36)

где Р₁ = ; Р₂ = .

Скорость или имеет знак «+», если её направление совпадает с

направлением оси Х, выбранным за положительное. Тогда направление скорости тела А положительно, а направление скорости для тела В отрицательно.

Знаки сил в уравнениях (36) определяются тем, совпадает ли вектор

данной силы с положительным направлением оси Х или противоположно ей.

По третьему закону Ньютона должно быть:

F₁ + F₂ = 0

или + = F₁ + F₂ = 0.

Отсюда следует, что P₁ + P₂ = const (37)

Таким образом, при взаимодействии двух тел сумма их импульсов является постоянной.

Третий закон Ньютона можно сформулировать как требование сохранения суммы импульсов взаимодействующих тел, если нет никаких других внешних сил. В этом его более глубокое физическое содержание.

Значение и содержание законов сохранения

Уравнения движения являются уравнениями изменения физических величин во времени и пространстве.

Законы сохранения отвечают на вопрос о том, что в последовательности физических ситуаций, описываемой уравнениями движения, остаётся неизменным и постоянным.

Рассмотрим уравнение Ньютона для одномерного случая, которое запишется в виде

а) ;

б) . (38)

Задача считается решённой, если известно положение движущейся точки в любой момент времени. Поэтому для решения надо проигнорировать уравнение. В этом заключается математическая сущность закона сохранения. Таким образом, в механике законы сохранения сводятся к первым интегралам уравнения движения. Законы сохранения фундаментальны и рассматриваются относительно системы материальных точек, если отсутствуют внешние силы. Такая система материальных точек или сил называется изолированной.

Однако изолированных в абсолютном смысле систем во Вселенной быть не может, так как все тела связаны силами тяготения.

С определёнными допущениями принимается, что в изолированной системе внешние силы отсутствуют, то есть F=0 , тогда . Интегрируя это равнение, получаем .

Значит, P_x = const, P_y = const, P_z = const. (39)

Равенство (39) выражает закон сохранения импульса: импульс изолированной системы не изменяется при любых процессах, происходящих внутри системы.

Для материальной точки закон сохранения импульса означает, что в отсутствие внешних сил она движется по прямой с постоянной скоростью.