Закон сохранения энергии. Если под действием силы изменяется абсолютное значение скорости, то говорят, что сила совершает работу

Если под действием силы изменяется абсолютное значение скорости, то говорят, что сила совершает работу. Если скорость увеличивается, то считается, что работа силы положительна, а если уменьшается, то отрицательна.

Рассмотрим случай, когда сила действует вдоль оси Х, и движение происходит вдоль этой оси.

Пусть материальная точка массы m₀ перемещается под действием силы сжатой пружины (рисунок 10), закреплённой в начале системы координат - точке 0.

Рисунок 10

Уравнение движения точки имеет вид

. (40)

Умножим обе части этого уравнения на 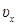и, учтя, что

= ,

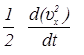получим ; (41)

так как , имеем . (42)

В этом виде равенство имеет очень наглядный смысл: при смещении точки на dx сила совершает над ней работу F_x×dx, в результате чего изменяется величина , характеризующая движение тел.

Величина называется кинетической энергией тела.

Если тело смещается из положения x₁ до x₂ , а его скорость при этом изменяется от 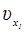до 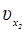, то, интегрируя, имеем

- = , (43)

то есть изменение кинетической энергии материальной точки при её перемещении между двумя положениями равно совершённой при этом работе.

Кинетическая энергия материальной точки изменяется, если силы не равны нулю. Кинетическая энергия остаётся постоянной в отсутствие сил, поэтому при F_x=0

= =сonst. (44)

Это закон сохранения кинетической энергии материальной точки.

При движении точки по произвольной траектории работа силы выражается как предел суммы элементарных работ на всём пути.

Тогда работа силы при перемещении вдоль произвольной траектории определяется так:

A = = . (45)

Интеграл криволинейный, взятый вдоль линии L.

Значит,

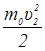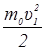- = . (46)

Последнее выражение - закон сохранения энергии, если иметь в виду не только механические формы энергии, так как в правой части равенства стоит величина, имеющая размерность энергии.

Например, если сила является силой трения, то интеграл в правой части выражает в определённых единицах степень нагревания среды, о которую производится трение.

Закон сохранения энергии позволяет сделать анализ движения без рассмотрения уравнения движения. При этом предполагается известным закон изменения потенциальной энергии.