
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Методические указания по решению задач к теме
"Законы Ньютона и законы сохранения"
При решении задач важно помнить, что второй закон Ньютона справедлив только в инерциальных системах отсчёта. Когда движение тел рассматривается относительно поверхности Земли, то систему отсчёта, связанную с Землёй, можно считать практически инерциальной.
Любая другая система отсчёта, которая движется поступательно и без ускорения относительно Земли, является инерциальной.
Задачи по динамике решаются по уравнению движения, выражающему второй закон Ньютона. При этом поступают поэтапно:
а) сделать чертёж и указать все силы, действующие на данное тело. Для правильного определения направления сил, действующих на тело, помнить, что сила тяжести направлена по линии отвеса.
Сила реакции опоры при отсутствии трения - по нормали к соприкасающимся поверхностям.
Сила натяжения нити направлена вдоль нити в сторону точки подвеса. Выражение на «тело действует сила» всегда означает, что данное тело взаимодействует с другим телом, в результате чего приобретает ускорение;
б) записать второй закон Ньютона в векторной форме;
в) если силы действуют не по одной прямой, то выбирают две взаимно перпендикулярные оси X и Y, лежащие в плоскости действия сил. Обычно рассматриваются лишь плоские системы сил.
Тогда второй закон Ньютона записывают в виде двух скалярных уравнений:
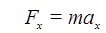 ,
, 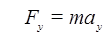 ; (47)
; (47)
г) если рассматривается движение системы связанных тел, то уравнения записываются для каждого тела. Кроме того, учитываются кинематические условия, связывающие ускорение отрицательных тел системы (например, равенство ускорений двух грузов, висящих на нерастяжимой нити, перекинутой через блок). То есть получают систему уравнений, число которых равно числу неизвестных величин, подлежащих определению;
д) при рассмотрении неинерциальной системы отсчёта необходимо учитывать силы инерции. Например, во вращающей системе отсчёта центростремительная –сила инерции. В инерциальной системе отсчёта на тела действуют силы инерции, внешние по отношению к данной системе тел. В этом случае система является неизолированной, поэтому и полная энергия системы, и полный импульс тела не сохраняются, так как и импульс, и энергия зависят от выбора системы отсчёта. Поэтому, составляя уравнения, выражающие законы сохранения импульса и энергии, необходимо рассматривать движение всех тел в одной и той же инерциальной системе отсчёта. Обычно это лабораторная система отсчёта, связанная с Землёй.
Если в условии задачи фигурирует относительная скорость двух движущихся тел, то целесообразно рассматривать явление в такой инерциальной системе отсчёта, в которой одна из частиц в этот момент неподвижна.
Закон сохранения импульса применяется при решении задач в том случае, когда связывают начальные и конечные значения импульса замкнутой системы тел, а закон взаимодействия между телами во времени неизвестен или сложен. Например, силы, возникающие при ударе. Закон сохранения импульса справедлив для замкнутых систем, и надо учитывать, что закон сохранения векторный, поэтому следует руководствоваться правилом сложения векторов.
Закон сохранения энергии применяют в том случае, когда рассматриваются потенциальные силы (гравитационные, упругие), изменяющиеся во времени. Применение закона сохранения энергии, связывающего начальное и конечное состояние системы взаимодействующих тел, упрощает решение, поскольку становится ненужным рассматривать закон изменения силы, действующей между телами. Закон сохранения механической энергии можно применять к системе взаимодействующих тел. При этом система должна быть замкнутой: внутри системы должны отсутствовать силы трения (кроме силы трения покоя) и силы неупругих деформаций, так как иначе механическая энергия системы рассеивается и превращается во внутреннюю энергию.
Если тело движется под действием силы тяжести, его нельзя считать изолированным. В этом случае изолированной системой, к которой можно применить закон сохранения энергии, будет система тело- Земля. При этом энергию Земли можно исключить из рассмотрения, так как само понятие потенциальной энергии тела в поле тяготения Земли предполагает энергию взаимодействия тела и Земли и уже, поэтому характеризует энергию всей системы, а не одного тела. Кроме этого, изменением кинетической энергии Земли в результате её взаимодействия с падающим телом можно пренебречь. Поэтому при решении задач на движение тела (или системы тел) в поле тяготения Земли не рассматривают ни потенциальную, ни кинетическую энергии Земли. При выборе нулевого уровня отсчёта высоты обычно принимают самое нижнее положение движущегося тела.
Дата добавления: 2015-02-10; просмотров: 316; Мы поможем в написании вашей работы!; Нарушение авторских прав |