Движение твердого тела. Поскольку угловое перемещение φ, угловая скорость и угловое ускорение связаны между собой так же

Поскольку угловое перемещение φ, угловая скорость и угловое ускорение связаны между собой так же, как и соответствующие им линейные величины , , , то методы решения задач на вращательное движение твёрдого тела во многом совпадают с теми, что рассмотрены для движения точки.

Если тело одновременно участвует в двух вращательных движениях с угловыми скоростям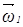и и относительно двух пересекающихся осей, то результирующее движение будет также вращательным с угловой скоростью, равной = 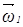+ . Направление вектора угловой скорости и вращения твёрдого тела связаны правилом правого винта.

Пример 4. Катающийся цилиндр остановлен силой 1 кг. Масса цилиндра 2 кг, путь торможения 0,5 м. Вычислить скорость цилиндра до торможения.

Решение:

Полная энергия катающегося тела равна сумме кинетических энергий поступательного и вращательного движений:

W = , (19)

где - I - момент инерции тела относительно оси, проходящей через центр

тяжести параллельно образующей;

- угловая скорость тела.

Момент инерции сплошного цилиндра относительно его оси равен

I = ,

где r - радиус цилиндра.

Линейная скорость точек поверхности качения

, то есть .

Подставим I и в (19): W = .

Кинетическая энергия цилиндра погашена работой силы торможения, то есть

F× S = .

Искомая скорость .

Вычисляем: м/с ;

м/с.

Пример 5.Две гири с массами m₁=2кг и m₂=1кг соединены нитью, перекинутой через блок массой m=1кг. Найти ускорение а, с которым движутся гири, и силы натяжения Т₁ и Т₂ нитей, к которым подвешены гири. Блок считать однородным диском. Трением пренебречь.

Решение:

Рисунок 6 – Пример 5

Запишем в векторной форме уравнения поступательного движения первой и второй гири

m₁ = m₁ 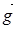+ ; m₂ = m₂ +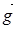

и уравнение вращательного движения диска

J× = + ,

где М₁ – момент силы натяжения нити Т₁,М₂ – момент силы натяжения нити Т₂.

Спроектируем первые два уравнения на ось х, а последнее на ось y и добавим уравнение кинематической связи. Получим систему 4-х уравнений:

m₁a = m₁g – T₁; (20)

-m₂a = m₂g – T₂; (21)

Je = RT₁-RT₂; (22)

a = eR. (23)

Подставим (23) в (22): J = R(T₁-T₂) (24)

Вычтем (21) из (20), подставим в полученное выражение (24) и найдем

а = 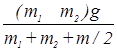= 2,8 м/с² (25)

Подставляя (25) в (20) и (21), получим

Т₁= m₁(g-a);

Т₁=14Н.

Т₂= m₂(g+a);

Т₂ = 12,6Н.

Пример 6.Блок массой m=1кг укреплен на конце стола. Гири 1 и 2 одинаковой массой m₁ = m₂ = 1 кг соединены нитью, перекинутой через блок. Коэффициент трения гири 2 о стол k =0,1. Найти ускорение a, с которым движутся гири, и силы натяжения Т₁ и Т₂ нитей. Блок считать однородным диском. Трением в блоке пренебречь.

Решение:

Рисунок 7 –Пример 6

Запишем второй закон Ньютона в проекциях на ось х и у:

где 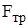=km₂g (28)

Разность сил (Т₁-Т₂) создает момент вращения, следовательно:

(Т₁-Т₂)R= ,

где J = ,

откуда Т₁-Т₂ = (29)

Из уравнений (26) – (28) найдем

Т₁= , (30)

Т₂= . (31)

Пусть m₁ = m₂ = m¢. Тогда Т₁-Т₂ = m¢(g – 2a – kg) = m¢g (1-k) - 2 m¢a, подставив (26), получим

mg (1-k) = + 2 m¢a = ,

откуда а = ;

a = 3,5 м/с².

Тогда из уравнения (30)

Т₁= 6,3 Н, Т₂= 4,5 Н.

Пример 7.Мальчик катит обруч по горизонтальной дороге со скоростью u =7,2 км/ч. На какое расстояние S может вкатиться обруч на горку за счет его кинетической энергии? Уклон горки равен 10м на каждые 100м пути.

Решение:

Рисунок 8 – Пример 7

У основания горки обруч обладал кинетической энергией W_k, которая складывалась из кинетической энергии поступательного движения и кинетической энергии вращения. Когда обруч вкатился на горку на расстояние S, его кинетическая энергия перешла в потенциальную. W_k = W_п.

W_k = + ;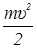

W_п = mgH.

Момент инерции обруча J=mR², частота вращения w = .

Тогда W_k = 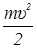+ = mu².

Следовательно, mu² = mgH,

откуда Н = .

Из рисунка видно, что = ,

откуда S = ,

или S = .

Подставив числовые данные с учетом u = 2 м/с, получим S = 4,1м.