Решение. Так как данный сигнал – периодическая функция времени, то для его спектрального представления нужно использовать или тригонометрический или комплексный ряд

Так как данный сигнал – периодическая функция времени, то для его спектрального представления нужно использовать или тригонометрический или комплексный ряд Фурье. Найдем спектры амплитуд и фаз на основе тригонометрического ряда Фурье.

Определим коэффициенты разложения сигнала на интервале t:= 0..T при угловой частоте основной гармоники ω₁:= и числе гармоник k:= 1..5.

1) Постоянная составляющая

2) Косинусоидальный коэффициент

Подстановка численных значений V_m, T и ω₁ дает

В результате интегрирования получим

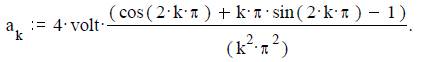
Например, a₁ = 0 volt; a₂ = 0 volt; a₃ = 0 volt; a₄ = 0 volt.

Более удобна другая форма определения коэффициентов разложения.

Так как

то выражая t₀ и ω₁ через T, имеем

Отсюда следует, что при k>0 коэффициенты a_k равны нулю.

3) Cинусоидальный коэффициент

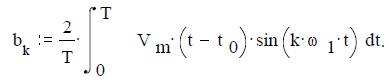
Выражая t₀ и ω₁ через T, можно получить

Отсюда после упрощений следует

Амплитуда k-й гармоники

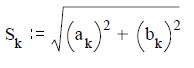
при k>1 будет

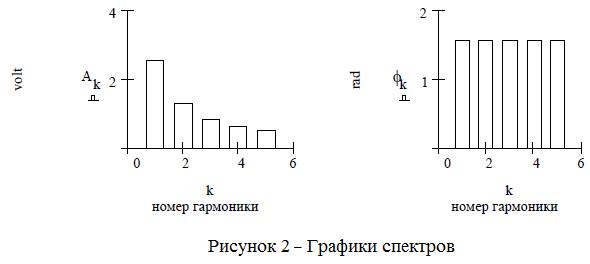
Таким образом, с учетом постоянной составляющей амплитудный спектр

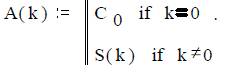
Фазовый спектр

Так как коэффициенты a_k=0 и b_k<0, и составит, например для k=1, φ = 1.571.

Графики данных спектров в виде столбчатых диаграмм приведены на рисунке 2.