Энергетические характеристики сигналов. Пусть сигнал x(t), задан на интервале наблюдения tm и есть напряжение (или ток) на сопротивлении R = 1 Ом

Пусть сигнал x(t), 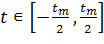задан на интервале наблюдения t_m и есть напряжение (или ток) на сопротивлении R = 1 Ом. Тогда при описании сигнала во временной области средняя мощность P и энергия E будут равны:

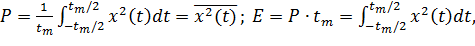(1.9)

где обозначение означает усреднение по времени квадрата сигнала.

Если допустить периодическое продолжение сигнала x(t) с периодом T = t_m , то среднюю мощность можно находить также, исходя из спектрального представления периодического сигнала в частотной области:

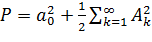–для ряда (1.1); (1.10)

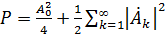–для ряд (1.2); (1.11)

–для ряда (1.3); (1.12)

Часто сигнал задается на бесконечном интервале [−∞,∞]. Тогда

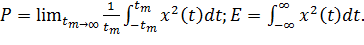(1.13)

Здесь различают два вида сигналов: энергетический или импульсный (E→E₀=const, Р→0) и мощностной (E→∞, Р→P₀=const).

Для энергетического сигнала справедливо равенство Парсеваля (или теорема Рейли)

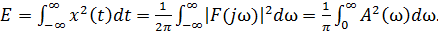(1.14)

Функция F(jω)²= A²(ω) = E(ω) называется спектральной плотностью энергии или энергетическим спектром. Она является четной функцией и определяет величину энергии, приходящейся на полосу в один рад/сек. Для мощностных сигналов рассматривают среднюю мощность, так как понятие энергии теряет смысл. Средняя мощность при t_m → ∞ будет

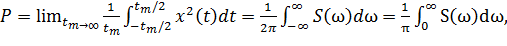(1.15)

где 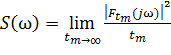– спектральная плотность мощности.

Для количественной оценки временного сдвига детерминированных сигналов используют автокорреляционную функцию АКФ

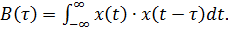(1.16)

Энергетический спектр и АКФ связаны преобразованием Фурье:

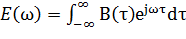(прямое преобразование); (1.17)

(обратное преобразование). (1.18)