
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
МАТРИЦЫ
МАТЕМАТИКА
Краткий курс лекций
Пермь, 2011г.
ЦЕЛЬ, ПРЕДМЕТ И ЗАДАЧИ ДИСЦИПЛИНЫ
«Математика» является основной дисциплиной цикла математических и естественнонаучных дисциплин.
Цели изучения дисциплины состоят в овладении студентами:
· базовыми знаниями в области математики как основы фундаментальных знаний;
· навыками решения задач;
· навыками самостоятельной работы с математической литературой.
Целью изучения также является формирование научного мировоззрения студентов.
Предмет дисциплины составляют основные понятия, определения, теоремы разделов математики и методы решения задач.
Задачи дисциплины состоят в обучении студентов:
· основным понятиям, определениям и теоремам разделов математики;
· умениям использовать полученные знания при решении задач и изучении общенаучных дисциплин и дисциплин специальности;
· умениям использовать систему знаний дисциплины для адекватного математического моделирования различных, в том числе экономических, процессов.
ТРЕБОВАНИЯ К УРОВНЮ ОСВОЕНИЯ ДИСЦИПЛИНЫ
В результате изучения дисциплины «Математика» студент должен:
а) иметь представление об основах:линейной алгебры; аналитической геометрии на плоскости и в пространстве; анализа бесконечно малых величин; дифференциального исчисления функций одной переменной; дифференциального исчисления функции нескольких переменных; интегрального исчисления функции одной и нескольких переменных; дифференциальных уравнений; теории рядов; теории вероятностей и математической статистики.
б) знать: основные понятия, теоремы, методы и правила решения типовых задач изучаемых разделов математики.
в) уметь: применять математические методы к решению теоретических и практических задач; применять полученные знания для решения задач общенаучных и специальных дисциплин.
г) приобрести навыки в решении задач и оценки полученных результатов.
д) владеть, иметь опыт использования необходимых вычислительных средств, таблиц и справочников при производстве расчётов.
Тезисы лекций
ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ
МАТРИЦЫ
Прямоугольная таблица чисел, содержащая т строк и п столбцов, называется матрицей размера тх п:  .
.
Каждый элемент матрицы снабжается двумя индексами: первый указывает номер строки, а второй – номер столбца, в которых расположен этот элемент.
Две матрицы называются равными, если числа их строк и столбцов совпадают и если равны элементы, расположенные на соответствующих местах этих матриц.
Если число столбцов матрицы п равно числу ее строк, то матрицу называют квадратной матрицей порядка п. Элементы 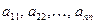 квадратной матрицы порядка п образуют ее главную диагональ.
квадратной матрицы порядка п образуют ее главную диагональ.
Квадратная матрица называется диагональной, если все ее элементы, расположенные вне главной диагонали, равны нулю. Диагональная матица называется единичной, если все ее элементы, расположенные на главной диагонали, равны единице.
Матрица  называется транспонированной для матрицы А если она получена из матрицы А путем перестановки местами строк и столбцов.
называется транспонированной для матрицы А если она получена из матрицы А путем перестановки местами строк и столбцов.
Действие над матрицами:
1) Умножение матрицы на число. Чтобы умножить матрицу на число, надо каждый элемент матрицы умножить на это число.
2) Сложение матриц. Суммой матриц А и В одинаковых размеров называется матрица, элементы которой равны суммам элементов матриц А и В, расположенных на соответствующих местах.
3) Умножение матриц. Матрицу А можно умножить на матрицу В только в том случае, когда число столбцов матрицы А равно числу строк матрицы В. В результате умножения получится матрица С, у которой столько же строк, сколько их матрице А, и столько же столбцов, сколько их в матрице В, а элементы матрицы С вычисляются по формуле:
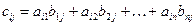 ,
,
т.е. для получения элемента 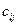 , расположенного в i-строке и j-омстолбце матрицы С, надо элементы i-ой строки матрицы А умножить на соответствующие элементы j-го столбца матрицы В и полученные произведения сложить.
, расположенного в i-строке и j-омстолбце матрицы С, надо элементы i-ой строки матрицы А умножить на соответствующие элементы j-го столбца матрицы В и полученные произведения сложить.
Дата добавления: 2015-02-10; просмотров: 290; Мы поможем в написании вашей работы!; Нарушение авторских прав |