
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ
- Производная и дифференциал функции
Предел отношения приращения функции к приращению ее аргумента, при стремлении последнего к нулю, называется производной функции в точке  :
:
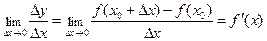 .
.
Из определения производной следует, что она представляет собой скорость изменения функции. В этом состоит ее механический смысл. В частности, скорость неравномерного прямолинейного движения есть скорость изменения расстояния по отношению ко времени: 
Геометрический смысл производной состоит в том, что производная функции представляет собой тангенс угла наклона касательной к графику этой функции в данной точке (х, f(x)), т. е. f ¢(x) = tg a.
Если функция y=f(x) имеет производную f¢(х) в точке х, то произведение производной f`(x) на приращение  аргумента называется дифференциалом функции:
аргумента называется дифференциалом функции: 
Дифференциал dx независимой переменной совпадает с ее приращением  . Поэтому можно записать: dy=f `(x)dx. Отсюда следует, что
. Поэтому можно записать: dy=f `(x)dx. Отсюда следует, что  т. е. производную f `(x) можно рассматривать как отношение дифференциала функции к дифференциалу независимой переменной.
т. е. производную f `(x) можно рассматривать как отношение дифференциала функции к дифференциалу независимой переменной.
Производные основных элементарных функций:
1.  ;
;
2.  ;
;
3.  ,
,  ;
;
4.  ,
, 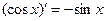 ,
,  ,
,  ;
;
5.  ;
;  .
.
Дата добавления: 2015-02-10; просмотров: 282; Мы поможем в написании вашей работы!; Нарушение авторских прав |