КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Функции двух независимых переменных
Частной производной функции z = f(x, у) по переменой х называется производная, вычисленная по обычным правилам дифференцирования в предположении, что у является постоянной величиной. Обозначается: 
.
Частной производной функции z = f(x, у) по переменой у называется производная, вычисленная по обычным правилам дифференцирования в предположении, что х является постоянной величиной. Обозначается: 
.
Дифференциалом функции двух независимых переменных называется выражение
.
Частные производные от частных производных называются частными производными второго порядка. Различают чистые частные производные, когда дифференцирование дважды осуществляется по одной переменной, и смешанные частные производные, когда дифференцирование осуществляется по разным переменным. Обозначаются: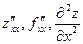 
; 
; 
; 
.
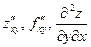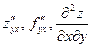Если частные производные первого порядка непрерывны, то значение смешанной производной не зависит от порядка дифференцирования.
Дата добавления: 2015-02-10; просмотров: 23; Нарушение авторских прав