
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
ПРДЕЛ ФУНКЦИИ
Число А называется пределом функции  в точке
в точке  , если при сколь угодно близком приближении аргумента
, если при сколь угодно близком приближении аргумента 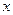 к значению
к значению  соответствующие значения функции сколь угодно близко приближаются к значению А. Обозначается:
соответствующие значения функции сколь угодно близко приближаются к значению А. Обозначается:  .
.
Число А называется правым (левым) пределом функции  в точке
в точке  , если при сколь угодно близком приближении аргумента
, если при сколь угодно близком приближении аргумента 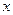 к значению
к значению  справа (слева) соответствующие значения функции сколь угодно близко приближаются к значению А. Обозначаются:
справа (слева) соответствующие значения функции сколь угодно близко приближаются к значению А. Обозначаются:  – правый предел,
– правый предел,  – левый предел.
– левый предел.
Теорема. Функция имеет предел в точке  тогда и только тогда, когда в этой точке существуют и равны между собой односторонние пределы функции. В этом случае значение предела совпадает со значением односторонних пределов.
тогда и только тогда, когда в этой точке существуют и равны между собой односторонние пределы функции. В этом случае значение предела совпадает со значением односторонних пределов.
Число А называется пределом функции  на бесконечности, если при неограниченном увеличении аргумента
на бесконечности, если при неограниченном увеличении аргумента 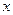 соответствующие значения функции сколь угодно близко приближаются к значению А. Обозначается:
соответствующие значения функции сколь угодно близко приближаются к значению А. Обозначается:  .
.
Справедливы следующие свойства пределов функции:
1. Если предел функции существует, то он единственный.
2. Предел постоянной величины равен самой постоянной.
3. Предел суммы (разности) функций равен сумме (разности) пределов функций.
4. Предел произведения функций равен произведению пределов функций.
5. Предел отношения функций равен отношению пределов функций.
При вычислении пределов функции используются замечательные пределы:
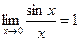 ;
;  .
.
Дата добавления: 2015-02-10; просмотров: 302; Мы поможем в написании вашей работы!; Нарушение авторских прав |