Интегрирование по частям. Пусть и - две функции. Тогда имеет место формула

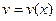Пусть и - две функции. Тогда имеет место формула

.

Замена переменных

Если подынтегральная функция представляет собой произведение функции сложного аргумента на производную этого аргумента, вычисленную с точностью до постоянной, то тогда выполнив замену сложного аргумента на новую переменную можно упростить интегрирование и свести его к непосредственному:

.

Определенный интеграл

Определенным называется интеграл вида . Если подынтегральная функции неотрицательна, то определенный интеграл равен по величине площади криволинейной трапеции, ограниченной графиком подынтегральной функции, прямыми , и осью абсцисс. Ниже перечислены основные свойства определенного интеграла.

1. ;

2. если 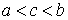, то ;

3. ;

4. ;

5. ;

6. если , то .

Вычисление определенных интегралов