
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Задание 12.
Исследовать сходимость числовых рядов 
| Вар. | а) un | б) un | Вар. | а) un | б) un |
| 12.1 | 
| 
| 12.6 | 
| 
|
| 12.2 | 
| 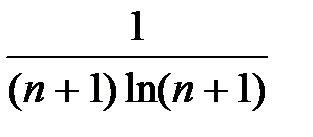
| 12.7 | 
| 
|
| 12.3 | 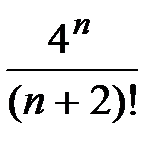
| 
| 12.8 | 
| 
|
| 12.4 | 
| 
| 12.9 | 
| 
|
| 12.5 | 
| 
| 12.10 | 
| 
|
Решение типового варианта контрольной работы
Алгебраическая форма комплексных чисел :

где i - мнимая единица; a - действительная часть: a = Re z; bi - мнимая часть
Действия над комплексными числами :
Если  то:
то:

Пример. Выполнить действия:
а) (2 + 3i)2; б) (3 – 5i)2; в) (5 + 3i)3.
Решение.
а) (2 + 3i)2 = 4 + 2*2*3i + 9i2 = 4 + 12i – 9 = – 5 + 12i;
б) (3 – 5i)2 = 9 – 2*3*5i + 25i2 = 9 – 30i – 25 = – 16 – 30i;
в) (5 + 3i)3 = 125 + 3*25*3i + 3*5*9i2 + 27i3;
так как i2 = – 1, а i3 = – i, то получим (5 + 3i)3 = 125 + 225i – 135 – – 27i = – 10 + 198i.
Задание 2
Найти обратную матрицу для 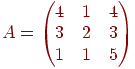 и выполнить проверку.
и выполнить проверку.
Решение
Вычисляем

следовательно, обратная матрица существует. Найдем присоединенную матрицу A*. Для этого вычислим все миноры второго порядка матрицы A и алгебраические дополнения:
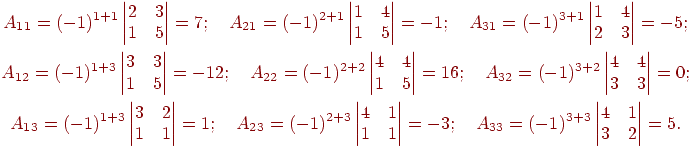
Составим

и найдем по формуле (2) обратную матрицу:

Проверка
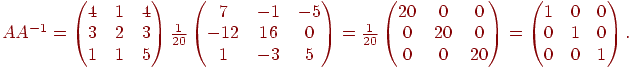
Дата добавления: 2015-02-10; просмотров: 292; Мы поможем в написании вашей работы!; Нарушение авторских прав |