Задание 3. Решить систему линейных алгебраических уравнений двумя способами: 1) по формулам Крамера;

Решить систему линейных алгебраических уравнений двумя способами: 1) по формулам Крамера;

2) методом Гаусса.

Решение: 1) По формулам Крамера решение системы находим в виде

, , ,

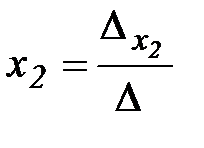где – основной определитель системы, а – вспомогательные определители, получаемые из основного заменой i-го столбца столбцом свободных членов. При система имеет единственное решение. При 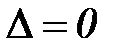решение следует искать другими методами.

Таким образом, имеем

.

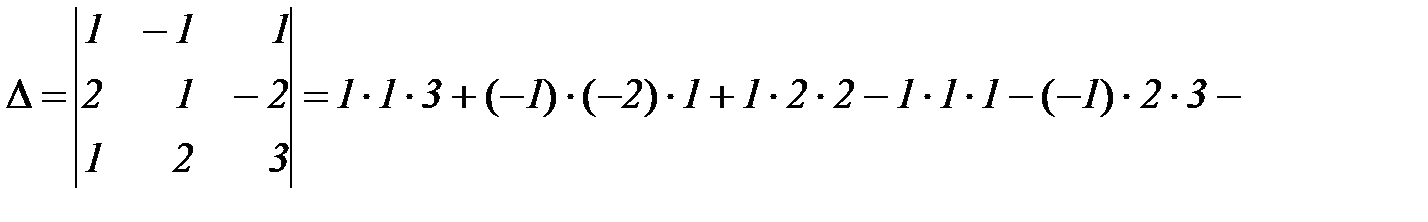
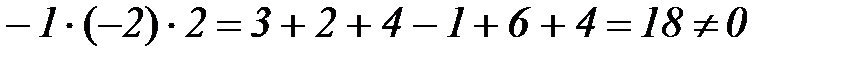Так как , то система имеет единственное решение. Найдем вспомогательные определители:

,

,

.

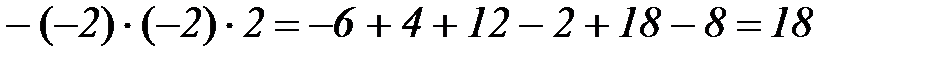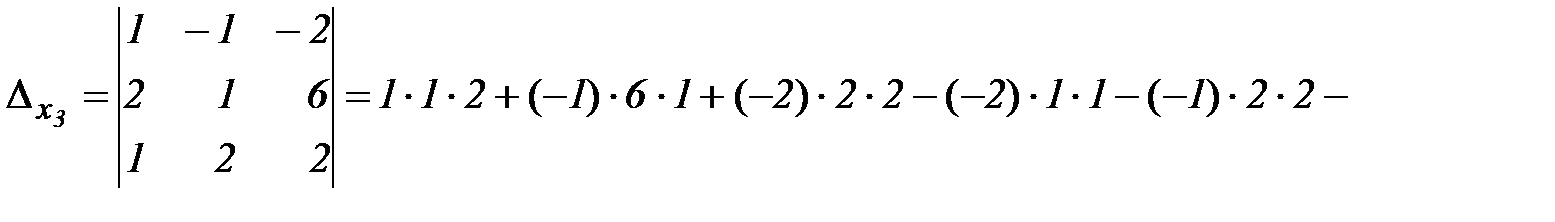
Тогда, , , .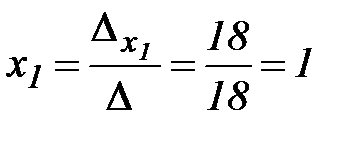

2) Для решения системы методом Гаусса составляется расширенная матрица системы, с которой можно проводить следующие действия:

а) все элементы какой-либо строки умножать или делить на одно и то же число;

б) к элементам какой-либо строки прибавлять соответствующие элементы другой строки, умноженные на одно и то же число.

Суть метода состоит в том, что с помощью этих преобразований, расширенная матрица сводится к треугольному или диагональному виду. Переходя обратно, от полученной матрицы к соответствующей системе, легко находим ее решение. Достоинство этого метода в том, что с его помощью можно решить любую систему линейных уравнений.

Составим расширенную матрицу данной системы и проведем преобразования:

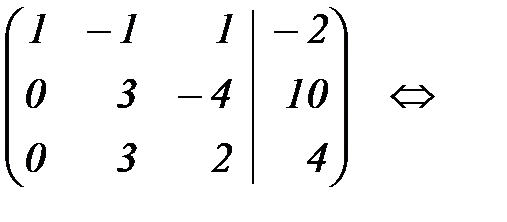
При первом переходе, к элементам второй и третьей строк прибавляли соответствующие элементы первой строки, умноженные на –2 и –1, соответственно. В результате получили в первом столбце первый элемент равный 1, а под ней все нули.

При втором переходе, к элементам третьей строки прибавляли соответствующие элементы второй строки, умноженные на –1. В результате получили во втором столбце третий элемент равный нулю. Матрица приобрела

треугольный вид. На этом прямой ход метода Гаусса закончен и можно перейти к системе, которая легко решается:

Но можно продолжить преобразования далее, получая нули и над элементами главной диагонали:

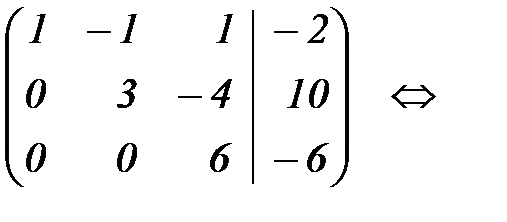
При первом переходе обратного хода метода Гаусса, элементы третьей строки разделили на 6, а затем к элементам первой и второй строк прибавляли соответствующие элементы полученной третьей строки, умноженные на –1 и 4, соответственно. В результате получили в последнем столбце последний элемент равный 1, а над ним все нули.

При втором переходе обратного хода метода Гаусса, элементы второй строки разделили на 3, а затем к элементам первой строки прибавляли соответствующие элементы полученной второй строки, умноженные на 1.

В результате получили все элементы главной диагонали равными 1, а остальные элементы равные нулю. Переходя к системе, получаем решение: