Задание 11

а) Найти частное решение ДУ удовлетворяющее условию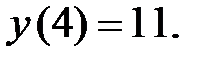

Разделяем переменные

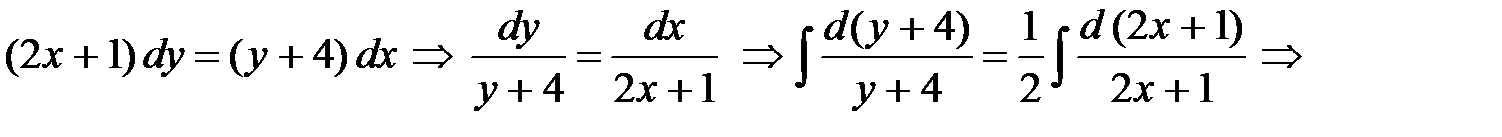
- общее решение данного уравнения.

Определим постоянную С так, чтобы выполнялось начальное условие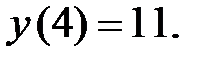

Получаем частное решение данного уравнения в виде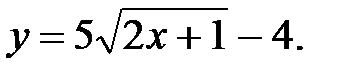

Линейное ДУ 1 порядка относительно функции 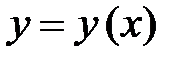и ее производной 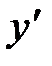имеет вид

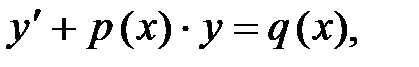(3)

где и 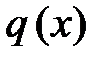- заданные непрерывные функции.

Заменой 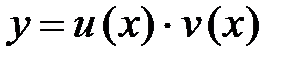решение ДУ (3) сводится к решению двух ДУ с разделяющимися переменными.

б)Найти частное решение ДУ 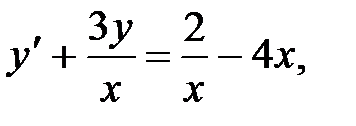(4)

удовлетворяющее начальному условию

Находим общее решение уравнения (4) с помощью замены Подставляем эту замену в уравнение (4)

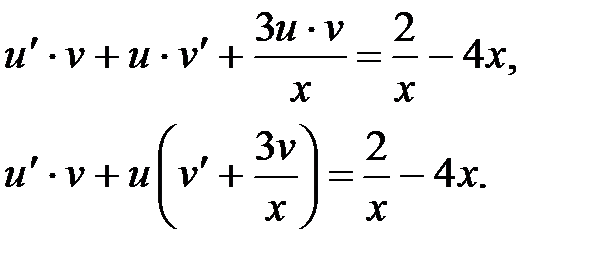
Функции и определяем из условий

Общее решение ДУ (4) имеет вид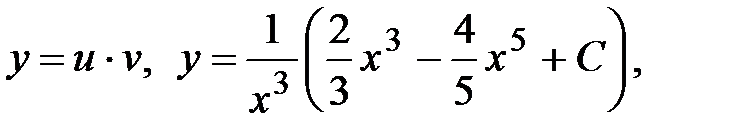

Определим С из начального условия

Искомое частное решение имеет вид

Задание 12

Исследовать числовые ряды на сходимость.

а)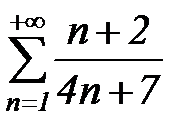

;

б)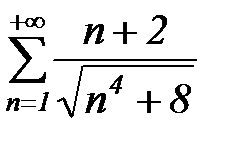

;

в)

;

Решение:

а) Мы имеем ряд . Его члены положительны и убывают. Найдем к чему стремится его n-ый член при стремлении n к бесконечности:

.

Значит, необходимое условие сходимости ряда не выполняется и ряд расходится.

б) Мы имеем ряд . Его члены положительны и убывают. Найдем к чему стремится его n-ый член при стремлении n к бесконечности:

.

Значит, необходимое условие сходимости ряда выполняется и ряд может как сходиться, так и расходиться.

Исследуем данный ряд по предельному признаку сравнения, согласно которому два ряда сходятся или расходятся одновременно, если . Так как в числителе максимальная степень n равна 1, а в знаменателе – 2, то сравнивать будем с гармоническим рядом ( ). Найдем предел отношения общих членов исходного и гармонического рядов при стремлении n к бесконечности:

.

Таким образом, по предельному признаку сравнения, исходный ряд и гармонический сходятся или расходятся одновременно. Так как гармонический ряд расходится, то расходится и исходный ряд.

в) Мы имеем ряд 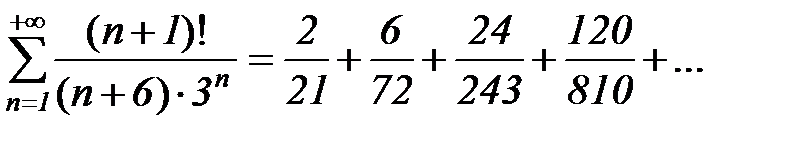. Его члены положительны и убывают. Так как в числителе общего члена ряда присутствует факториал, а в знаменателе степень, то при проверке стремления этого члена при стремлении n к бесконечности получим довольно сложный предел:

,

то вычислять его не будем.

Исследуем данный ряд на сходимость по предельному признаку Д’Аламбера: если , то при данный ряд сходится, при ­– расходится, при ­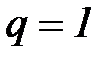– требуется исследовать по другим признакам.

Поскольку , , то

.

Следовательно, данный ряд расходится.