Логический квадрат

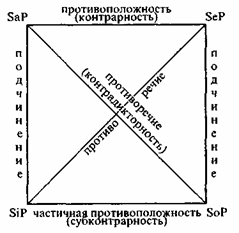
“Логический квадрат” представляет собой наглядную схему взаимного отношения суждений четырех типов А, Е, I, О. Строится логический квадрат так: левый верхний угол обозначается буквой А (общеутвердительное суждение) или SaP; правый верхний угол обозначается буквой Е (общеотрицательное суждение) или SeP; нижний левый угол обозначается буквой I (частноутвердительное суждение) или SiP; нижний правый угол обозначается буквой О (частноотрицательное суждение) или SoP.

Каждая линия, соединяющая выделенные типы суждений, представляет определенное отношение между двумя типами суждений. Византийский логик XI в. Михаил Пселл, предложивший “логический квадрат”, обратил внимание на то, что, зная истинность или ложность одного суждения в схеме “логического квадрата”, можно сделать вывод об истинности или ложности другого суждения.

В самом деле, мы уже знаем закон противоречия, который был использован нами в логике высказываний: противоречащие друг другу высказывания не могут быть вместе истинными. Если я высказываю общеутвердительное суждение SaP “Все студенты хорошо подготовились к зачету”, то, утверждая истинность общеутвердительного суждения, тем самым отрицаю истинность частноотрицательного суждения SoP “Некоторые студенты не подготовились к зачету”. И, наоборот, утверждая истинность частноотрицательного суждения, я отрицаю истинность общеутвердительного суждения.

То же будем иметь, если я буду утверждать истинность общеотрицательного суждения SeP. Тем самым я не признаю истинность частноутвердительного суждения SiP “Некоторые студенты подготовились к зачету по логике”.

Итак, противоречащими друг другу суждениями будут пары суждений А и О и Е и I. Они, в соответствии с законом противоречия, не могут быть одновременно истинными. И, тем более, не могут быть одновременно истинными контрарные (противоположные) суждения А и Е (А: “Все студенты подготовились к зачету” и Е: “Ни один студент не подготовился к зачету”).

Все сказанное нами дает возможность сделать следующий вывод об истинности суждений:

если истинно А, то ложно О и ложно Е;

если истинно Е, то ложно I и ложно А;

если истинно I, то ложно Е;

если истинно О, то ложно А.

Теперь попробуем рассуждать от ложности. Здесь мы должны воспользоваться законом исключенного третьего. Этот закон запрещает одновременную ложность противоречащих друг другу суждений.

Отсюда мы должны сделать следующий вывод:

если ложно А, то истинно О;

если ложно О, то истинно А;

если ложно Е, то истинно I;

если ложно I, то истинно Е.

К этим выводам можно добавить вывод, полученный косвенно: например, пусть А истинно. Что можно сказать об истинности I? Нетрудно доказать с помощью наших законов мышления, что истинность общего суждения будет обозначать истинность частного суждения.

Если истинно А, то на основании закона противоречия будет ложным Е. Но если ложно Е, то на основании закона исключенного третьего будет истинно I. Значит, если истинно А, то истинно I. Аналогично можно доказать, что истинность Е обуславливает истинность О.

В самом деле, если Е истинно, то, на основании закона противоречия, А ложно. Если А ложно, то на основании закона исключенного третьего, О истинно. Значит, если истинно Е, то истинно О.

Отсюда следует общий вывод: если общее суждение А или Е истинно, то будет истинным и подчиненное им частное суждение, соответственно, I и О. Здесь следует еще раз напомнить читателю, что термин “некоторые” в логике суждений используется не в смысле “некоторые, но не все”, а в смысле “некоторые, может быть, и все”.

Далее, рассмотрим те высказывания, которые могут быть получены из ложности частных суждений. Допустим, I — ложно. Тогда, на основании закона исключенного третьего, Е истинно. На основании закона противоречия в этом случае А ложно. Применяя закон исключенного третьего к противоречащему суждению, получим, что О истинно.

Значит, мы получили вывод о том, что ложность частного суждения 1 обуславливает ложность общего А и истинность субконтрарного суждения О.

Соответственно, если ложно О, значит, истинно А и ложно Е, и истинно I.

Значит, ложность частного суждения О обуславливает ложность общего суждения Е и истинность субконтрарного суждения 1.

Из этого следует, соответственно, два вывода:

1) ложность частного суждения обуславливает ложность общего суждения;

2) ложность частного суждения обуславливает истинность субконтрарного частного суждения.

Мы рассмотрели все выводы, которые можно получить по схеме “логического квадрата”. Однако, важно так же иметь в виду те выводы, которые нельзя получить.

Нельзя получить вывод от ложности общего к ложности частного суждения.

Нельзя получить вывод от истинности частного суждения к истинности общего суждения.

И, наконец, нельзя перейти от ложности общего к истинности контрарного (противоположного) суждения, т. е. нельзя распространять закон исключенного третьего на контрарную противоположность.

Если ложно А, то отсюда никак не следует истинность Е, так же, как из ложности Е не следует истинность А.

Известен с древних времен так называемый парадокс Эпименида, который был критянином. И он сказал: “Все критяне лгуны”. Поскольку он критянин, то, оказывается, что и он лгун. Значит, критянин говорит правду. Следовательно, он — лжец, поскольку его утверждение, что “Все критяне лгуны” — ложно. А раз оно ложно, то значит, критяне говорят правду. И он, как критянин, говорит правду. Значит, что “все критяне — лгуны” — истинно.

Одно и то же суждение и истинно, и ложно, и это противоречит нашим законам мышления.

Зная изложенные выше правила, относящиеся к законам мышления, нам легко разобраться в этом парадоксе. Пусть утверждение “Все критяне лгуны” — ложно. Это общеутвердительное суждение А. Однако, в соответствии с законом исключенного третьего, из ложности А никоим образом не следует, что критяне говорят правду, т. е. истинность Е (Ни один критянин не лгун). Может быть, какие-то критяне не лгуны, и тогда парадокс исчезает.

Отметим, что столь простое исчезновение парадокса лжеца возможно лишь в том случае, когда он дан в приведенной выше форме (парадокс Эпименида). Значительно более сложной является ситуация парадокса Эвбулида: “То, что я сейчас вам говорю, — ложь”! Однако, есть попытки решения парадокса и в этом случае.