Общие понятия. В теории изгиба расчет на прочность балок дополняется расчетом на жесткость

В теории изгиба расчет на прочность балок дополняется расчетом на жесткость. При этом оценивается упругая податливость балки и определяются такие её размеры, при которых возникающие деформации не превышали бы допустимых пределов. Тогда условие жесткости можно представить в таком виде:

где f_max – максимальная расчетная деформация (линейная или угловая);

[f] – допускаемая деформация.

Рассмотрим основные параметры деформированного состояния нагруженной балки (рисунок 2.1).

Упругая линия (у.л.) – искривленная ось балки под действием нагрузки.

Прогиб (y) –– линейное перемещение центра тяжести сечения, отсчитываемое перпендикулярно к исходной оси балки, м.

Горизонтальное смещение (u) балки, обычно бесконечно малая величина, принимаемая равной 0.

Угол поворота (θ) – угловое перемещение сечения относительно начального положения (иногда может определяться как угол между касательной к упругой линии и исходной осью), град, рад.

При изгибе балки для линейных и угловых перемещений (y и θ) принимают следующие правила знаков (рисунок 2.2):

- прогибy считается положительным, если перемещение точки происходит вверх, т.е. в направлении оси у;

- угол поворота θ считается положительным при повороте сечения против часовой стрелки (это справедливо для правой системы координат, для левой-наоборот).

Между прогибом и углом поворота существует дифференциальная зависимость, которую можно получить рассматривая бесконечно малые координаты некоторой плоской кривой (рисунок 2.3).

(2.2)

На основании (2.3) угол поворота в данном сечении равен производной прогиба по абсциссе сечения.

Таким образом, для нахождения линейных или угловых деформаций в реальных балках необходимо знать её уравнение упругой линии (УУЛБ), которое в общем виде можно представить как функцию от абсциссы сечения

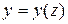. (2.4)

Рассмотрим методы нахождения деформаций при изгибе, основанные на составлении и решении уравнения упругой линии балки.