Способ Верещагина и его применение

Предлагаемый способ является графо-аналитическим способом решения интеграла Мора, который заключается в «перемножении» эпюр изгибающих моментов по силовым участкам заданной системы. Такое решение возможно благодаря тому, что для систем, имеющих прямолинейные участки, эпюра изгибающих моментов от единичной нагрузки имеет линейные очертания (прямоугольник, треугольник, трапеция).

Согласно способу Верещагина искомое перемещение представляет собой произведение площади грузовой эпюры на ординату единичной эпюры, которая располагается под центром тяжести грузовой эпюры на данном участке (рисунок 2.10). Формула Верещагина имеет такой вид:

где ω_i – площадь грузовой эпюры на участке i.

– ордината единичной эпюры под центром тяжести грузовой эпюры на участке i.

Рассмотрим пример определения перемещения по способу Верещагина (рисунок 2.11); найдем угол поворота в точке В (θ_B ). Предварительно выполним операции нагружения вспомогательной балки аналогично методу Мора. Построим эпюры изгибающих моментов от внешних нагрузок и единичного момента. Перемножением полученных эпюр находим угол поворота в точке В:

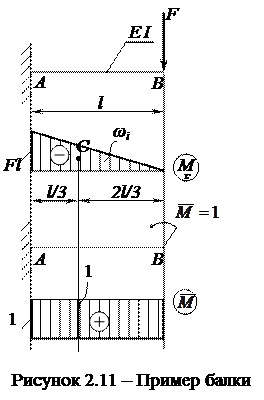
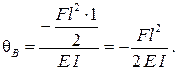
Знак «минус» указывает на то, что угловое перемещение в искомой точке направлено в сторону, противоположную действию фиктивного единичного момента, т.е. сечение балки поворачивается по ходу часовой стрелки.

При применении способа Верещагина, с целью упрощения расчетов рекомендуется использовать следующие замечания:

1) При перемножении эпюр, имеющих линейные очертания, можно перемножать площадь одной из них на ординату другой в прямой и обратной последовательности

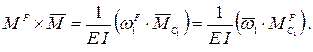
2) Если перемножаемые эпюры имеют сложную форму, то их можно разбивать на простые части и перемножать по отдельности (рисунок 2.12), т.е.

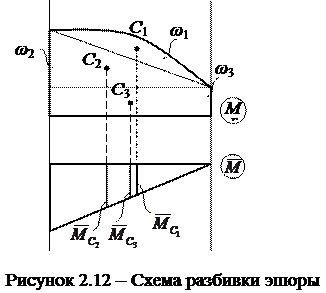3) В некоторых случаях сложные эпюры удобно перемножать, используя прием «расслоения эпюр». В этом случае в пределах данного участка строятся эпюры от каждой нагрузки в отдельности, которые перемножаются поочередно с единичной эпюрой.

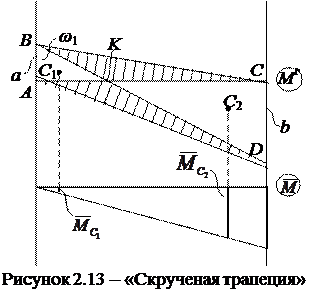4) Если одна из эпюр имеет форму «скрученной трапеции», то ее дополняют до двух треугольников, которые перемножаются по отдельности с другой эпюрой (рисунок 2.13)

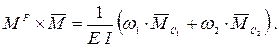
5) Когда обе эпюры имеют сложную форму, их можно перемножать по формуле Симпсона, предварительно определив ординаты эпюр моментов в левом (М_лев), среднем (М_ср) и правом (М_прав) сечениях:

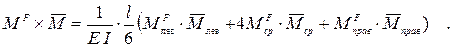
Здесь ордината в среднем сечении параболической эпюры моментов определяется по формуле

здесь знак «+» выбирается в случае, когда распределенная нагрузка направлена вниз, а знак «-», когда – вверх.

Способ Верещагина является достаточно удобным и простым для расчета перемещений в упругих системах при любых видах деформаций. Однако его нельзя применить для систем, имеющих криволинейные участки.

В завершение следует заметить, что рассмотренные выше методы определения перемещений при изгибе широко используются не только при нахождении перемещений в упругих системах, но и применяются при расчете статически неопределимых систем.