Расчет СНС. Каноническое уравнение метода сил (КУМС)

Для решения СНС при изгибе применяются метод сил, метод перемещений и комбинированный метод. В курсе сопротивления материалов широко применяется метод сил, в частности, прием сравнения перемещений, канонические уравнения метода сил и уравнение трех моментов для многопролетных балок.

Расчет СНС при изгибе по методу сил сводится к получению и решению дополнительных уравнений перемещений, в качестве которых составляются уравнения равенства нулю перемещений точек, где действуют «лишние связи» системы. Такие уравнения перемещений удобно записывать по определенному правилу – канону, поэтому их называют каноническими уравнениями метода сил (КУМС).

Для каждой лишней связи (опоры) составляется уравнение деформаций в виде суммы перемещений, вызванных действиями всех лишних связей (D_1Х) и внешних нагрузок (D_1F), причем эти деформации на опорах должны равняться нулю:

В общем случае КУМС для n –раз неопределимой системы записывается так:

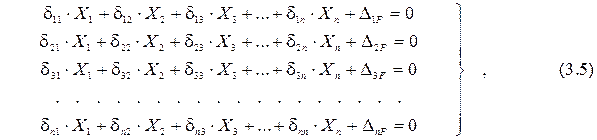
где δ₁₁, δ₂₂, δ₃₃, ... δ_nn – главные коэффициенты КУМС, представляющие собой единичные перемещения в i-й точке под действием единичной силы, приложенной в той же точке; они определяются по способу Верещагина путем перемножения эпюр от единичных сил «самих на себя»:

δ₁₂, δ₁₃, ... δ_ij – побочные коэффициенты, представляющие собой перемещения в i^той точке под действием единичной силы, приложенной к j-й точке; определяемые по способу Верещагина путем перемножения единичных эпюр между собой:

Δ_1F, Δ_2F, ... Δ_nF – грузовое перемещение, определяемое как перемещение в i^той точке под действием системы внешних нагрузок; по способу Верещагина оно находится путем перемножения грузовой эпюры моментов на единичную эпюру под действием i-й единичной силы

После нахождения всех единичные и грузовых перемещений КУМС, решается данная система и определяются неизвестные усилия X₁; X₂; X₃ ... X_i ... X_n.

По завершении раскрытия неопределимости СНС обычными приемами строятся необходимые эпюры (для рамы – N, Q и M). В завершении выполняются две проверки – статическая и деформационная.

Статическая проверка заключается в проверке условий равновесия элементов или узлов системы (например, методом вырезания узлов для рамы).

Деформационная проверка сводится к расчету перемещений тех точек системы, где отбрасывались лишние связи (X_i). Обычно проверяется равенство нулю перемещений в опорах системы. Для этого необходимо по способу Верещагина перемножить конечную эпюру изгибающих моментов с единичной эпюрой, построенной для i-й лишней связи, т.е.