Дифференциальное уравнение упругой линии балки и его интегрирование

Деформации точек балки обусловливаются искривлением ее изогнутой оси, т.е. зависят от ее кривизны. Из теории изгиба известна зависимость кривизны балки от изгибающего момента и жесткости сечения

С другой стороны из курса высшей математики кривизна плоской кривой может быть представлена через её координаты следующим образом:

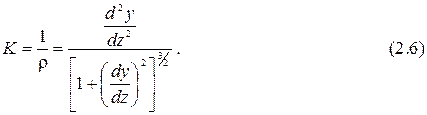
Приравнивая правые части выражений (2.5) и (2.6), получим точное дифференциальное уравнение упругой линии балки (ДУУЛБ)

Полученное нелинейное дифференциальное уравнение второго порядка вызывает большие трудности при решении. Поэтому его упрощают, учитывая, что в реальных конструкциях углы поворота не превышают 1⁰. Тогда знаменатель правой части выражения (2.7) будет мало отличаться от единицы, т.е.

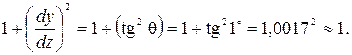
В итоге получают следующее приближенное ДУУЛБ, которое будет называться в дальнейшем основным дифференциальным уравнением упругой линии балки

Данное уравнение справедливо для малых деформаций и правой системы координат.

Полученное уравнение (2.8) решается путем последовательного двойного интегрирования.

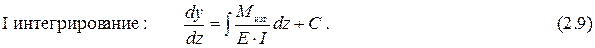
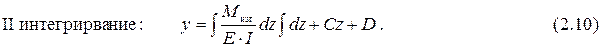
В этом решении произвольные постоянные интегрирования С и D представляют собой (по геометрическому смыслу) соответственно угол поворота и прогиб в начале координат

Произвольные постоянные интегрирования определяются из граничных или начальных условий построения расчетной схемы балки. Рассмотрим основные разновидности граничных условий.

Для простой балки (рисунок 2.4) граничные условия определяются из схемы закрепления на шарнирных опорах, где прогибы отсутствуют, т.е.

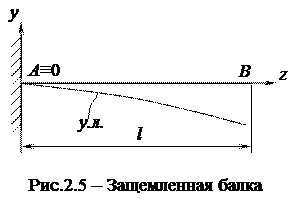Для защемленной балки (рисунок 2.5) нулевыми являются прогиб и угол поворота в заделке, т.е.

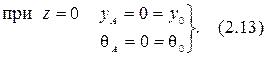
Для двухконсольной балки (рисунок 2.6) прогибы в шарнирных опорах также отсутствуют, т.е.

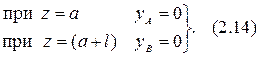
Рассмотренный выше метод расчета перемещений при изгибе называется методом непосредственного интегрирования дифференциального уравнения упругой линии балки (МНИ ДУУЛБ).

Для его применения необходимо выполнить следующее:

- выбрать систему координат (в крайнем сечении балки);

- для каждого силового участка балки составить общее уравнение моментов и подставить его в основное ДУУЛБ;

- решить ДУУЛБ путем двойного интегрирования и определить произвольные постоянные интегрирования из граничных условий;

- в полученное УУЛБ подставить абсциссы искомых точек и определить искомые прогибы;

- аналогично найти угловые перемещения, используя уравнение углов поворота.

Метод непосредственного интегрирования ДУУЛБ является достаточно простым и наглядным способом нахождения перемещений в балках. Однако он обладает существенным недостатком, заключающимся в том, что для расчета балок с большим количеством силовых участков необходимо определить значительное количество произвольных постоянных интегрирования. Так, например, для балки, имеющей n – участков, необходимо определить 2n – произвольных постоянных. Поэтому данный метод целесообразно использовать только для балок, имеющих один или два участка. Указанный недостаток можно исключить путем применения более совершенного приема составления и решения ДУУЛБ.