Потенциальная энергия упругой деформации в общем случае нагружения бруса. Теорема Кастильяно

На основании закона сохранения энергии считается, что работа внешних сил (Р) на перемещениях точек системы (d) переходит в потенциальную энергию ее упругой деформации (U), т.е.

Основываясь на положениях этого закона, можно, зная величину потенциальной энергии упругой деформации (ПЭУД), накопленной брусом, найти перемещение ее точек при известных внешних нагрузках. Общая зависимость для ПЭУД произвольно нагруженного бруса, находящегося под воздействием разнообразных внешних нагрузок, определяется как сумма работ, совершаемых шестью внутренними силовыми факторами:

После подстановки известных зависимостей работ для простых деформаций можно получить общее выражение для нахождения ПЭУД:

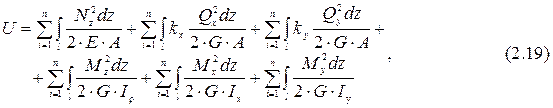
где k_x, k_y – безразмерные коэффициенты, характеризующие форму

сечения бруса при сдвиге.

Для нахождения перемещений с помощью ПЭУД применяется так называемая теорема Кастильяно: обобщенное перемещение точки приложения некоторой обобщенной нагрузки по направлению ее действия представляет собой частную производную потенциальной энергии деформации по этой нагрузке:

где δ_k – обобщенное перемещение в точке к , где приложена внешняя обобщенная нагрузка;

F_K – обобщенная нагрузка, действующая в точке к.

Под обобщенным перемещением понимается тот вид перемещения, на котором соответствующая обобщенная нагрузка совершает работу. В частности, при действии сосредоточенной силы работа производится на линейном перемещении, а при действии момента – на угловом перемещении :

Недостатком теоремы Кастильяно является то, что она позволяет находить только перемещения, соответствующие данной обобщенной нагрузке, только в точке её приложения и только по направлению ее действия. Этот факт существенно ограничивает область ее применения для реальных конструкций. Поэтому предлагаются приемы по совершенствованию теоремы Кастильяно.