Билет №3. 1. Упростить так, чтобы полученное выражение не содержало вхождений букв А, В, С.

1. Упростить так, чтобы полученное выражение не содержало вхождений букв А, В, С.

2. Доказать с помощью таблицы истинности, что (A®B)Ú (A®C) º A® (BÚC).

3. Пусть A – множество различных букв, входящих в Вашу фамилию, В – множество всех гласных букв в алфавите. Задать множества A, B,AÈB, AÇB, A\B, B\A перечислением элементов.

4. Упростить релейно-контактную схему и записать условие проводимости.

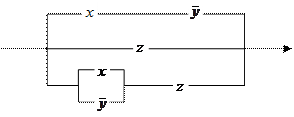5. Доказать, что формула В является логическим следствием формул .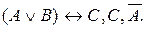

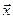6. Пусть – длина вектора . На множестве векторов V определены отношения:

а) ,

б) ,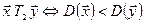

в) .

Какие из этих отношений являются эквивалентностью или порядком? В первом случае охарактеризовать классы эквивалентности, во втором – определить тип порядка.

7. Доказать, что бинарное отношение 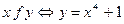есть отображение 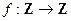и отображение 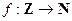. Будет ли каждое из этих отображений инъективным, сюръективным, обратимым?

8. Сколькими существует девятизначных чисел, у которых все цифры различны?