Билет №11. 1. Доказать и проиллюстрировать диаграммой Венна, что (A\B)\C Í (A\B)\(B\C)

1. Доказать и проиллюстрировать диаграммой Венна, что (A\B)\C Í (A\B)\(B\C)

2. Упростить формулу AÚ .

3. Пусть A – множество различных букв, входящих в Вашу фамилию, В – множество всех гласных букв в алфавите. Задать множества A, B,AÈB, AÇB, A\B, B\A перечислением элементов.

4. Упростить релейно-контактную схему и записать условие проводимости.

5. Доказать, что 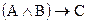является логическим следствием формулы

6. На множестве всех точек прямой определены отношения:

а) 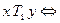«х совпадает с у»,

б) «х предшествует у»,

в) «х предшествует или совпадает с у».

Какие из этих отношений являются эквивалентностью или порядком? В первом случае охарактеризовать классы эквивалентности, во втором – определить тип порядка.

7. Пусть А – множество всех трехзначных натуральных чисел, 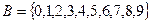. Доказать, что бинарное отношение «у – вторая цифра в десятичной записи х» есть отображение 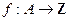и отображение 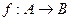. Будет ли каждое из этих отображений инъективным, сюръективным, обратимым?

8. Сколько можно составить шестизначных чисел, которые не делятся на десять и имеют различные цифры?