Билет №12.

1. Доказать и проиллюстрировать диаграммой Венна, что (AÈC)\(BÈC) Í (A\B)ÈC

2. Доказать с помощью таблицы истинности, что (A®B)Ú (A®C) º A® (BÚC).

3. Пусть U-множество всех четырехугольников плоскости, Р–множество прямоугольников, R – множество всех ромбов, Т – множество всех трапеций. Задать множества PÈR, PÇ , RÇT, указанием характеристического свойства.

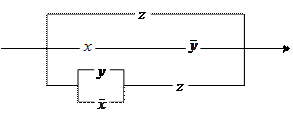
4. Упростить релейно-контактную схему и записать условие проводимости.

5. Является ли логическим следствием формулы ?

6. Пусть – периметр треугольника х. На множестве всех треугольников определены отношения: а) ,

б) ,

в) .

Какие из этих отношений являются эквивалентностью или порядком? В первом случае охарактеризовать классы эквивалентности, во втором – определить тип порядка.

7. Доказать, что бинарное отношение есть отображение 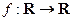и отображение , где . Будет ли каждое из этих отображений инъективным, сюръективным, обратимым?

8. Сколько существует способов сформировать футбольную команду (11 человек) из имеющихся 14 человек так, чтобы Иванов обязательно входил в ее состав?