Билет №21.

1. Доказать и проиллюстрировать диаграммой Венна, что (A\B)\C Í (A\B)\(B\C)

2. Доказать с помощью таблицы истинности, что .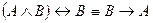

3. Пусть А – множество целых решений неравенства 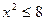, В – множество натуральных решений неравенства . Задать перечислением элементов множества A, B,AÈB, AÇB, A\B, B\A.

4. Упростить релейно-контактную схему и записать условия проводимости.

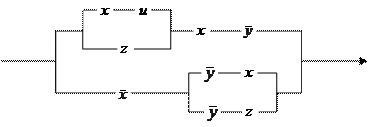5. Доказать, что 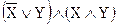является логическим следствием формул

6. На множестве участников шахматного турнира определены отношения:

а) 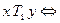«х набрал столько же очков, что и у»,

б) «х набрал больше очков, чем у»,

в) «х не меньше очков, чем у».

Какие из этих отношений являются эквивалентностью или порядком? В первом случае охарактеризовать классы эквивалентности, во втором – определить тип порядка.

7. Доказать, что отношение есть отображение 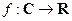и отображение , где . Будет ли каждое из этих отображений инъективным, сюръективным, обратимым?

8. Во скольких точках пересекаются 10 прямых линий, если между ними нет параллельных прямых и через каждую точку пересечения проходит не более двух прямых?