Построение графика перемещений толкателя

Известны следующие параметры: безмасштабный график скорости толкателя (рис. 4.1), ход (максимальное перемещение) толкателя S=75 мм – для кулачкового механизма с поступательно движущимся толкателем и =40˚ (0,7 рад) – для кулачкового механизма с качающимся толкателем, угловая скорость кулачка =100 1/с.

Требуется построить график перемещений толкателя.

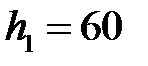Изображаем график скорости толкателя таким образом, чтобы горизонтальная ось N (или t), обозначающая номера положений механизма (или время), имела длину L=240 мм (в нашем случае из-за небольшого формата бумаги L=120 мм), а максимальная ордината была равной мм (в данном случае мм). Для правильного построения графика перемещений необходимо, чтобы суммарная площадь фигур, расположенных над осью N, была бы равна площади фигур, расположенных под осью N. В рассматриваемом случае площадь треугольника равняется площади трапеции. Находим площади этих фигур по известным формулам и приравниваем их

.

Отсюда высота трапеции

мм.

Для графика перемещений выбираем максимальную ординату (или ), например, мм (рис 4.2). Находим площадь треугольника

мм².

Тогда масштабный коэффициент площади будет равен

.

Разбиваем график скоростей на 12 интервалов и определяем площади фигур для каждого интервала, замеряя высоты и основания треугольников и трапеций.

, , , , , , , , , , , .

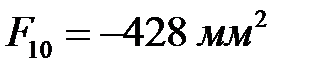(Площади под осью N отрицательны).

Находим ординаты на графике перемещений

, ,

,

,

, ,

, , ,

, , .

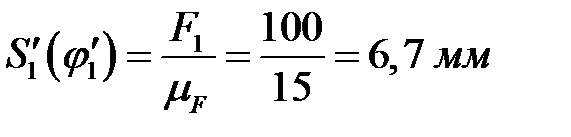Полученные ординаты откладываем от оси N и через найденные точки проводим плавную кривую, являющуюся графиком перемещений толкателя (рис. 4.2).

Определяем масштабные коэффициенты и

, .

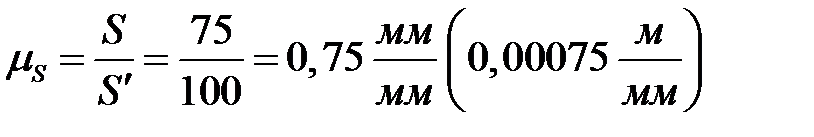Для нахождения коэффициентов и 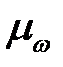воспользуемся формулами

, .

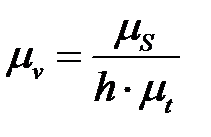Здесь – масштабный коэффициент времени, который определяется из формулы

.

Величина (рис. 4.2) находится следующим образом. На графике перемещений в любой точке проводим касательную . Точку сносим на ось 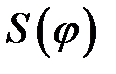, получая точку , через которую проводим луч, параллельный касательной. Луч пересекает ось N в точке . Расстояние от точки до начала координат и есть величина мм.

Для нашего случая получаем

, .