
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Синтез центрального кулачкового механизма с поступательно движущимся толкателем
Известны следующие параметры механизма: график перемещений толкателя (рис. 4.2), минимальный радиус кулачка 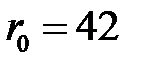 мм, радиус ролика
мм, радиус ролика 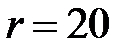 мм, ход толкателя
мм, ход толкателя  мм, скорость кулачка
мм, скорость кулачка  1/с, направление вращения кулачка – против часовой стрелки.
1/с, направление вращения кулачка – против часовой стрелки.
Требуется построить профиль кулачка.
Выбираем масштабный коэффициент кулачкового механизма  . Это значит, что механизм будет изображен уменьшенным в 1,5 раза.
. Это значит, что механизм будет изображен уменьшенным в 1,5 раза.
Находим размеры на чертеже
 ,
,  .
.
Из произвольной точки О (рис 4.3) проводим окружность радиуса  мм, которую делим на 12 частей, причем нумерацию точек
мм, которую делим на 12 частей, причем нумерацию точек  ведем в направлении, обратном направлению вращения кулачка. В нашем случае – по часовой стрелке. На продолжении луча
ведем в направлении, обратном направлению вращения кулачка. В нашем случае – по часовой стрелке. На продолжении луча  откладываем расстояние
откладываем расстояние  . На продолжении луча
. На продолжении луча 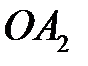 откладываем величину
откладываем величину  и т.д. Точки
и т.д. Точки  соединяем плавной кривой, которая представляет собой центровой (теоретический) профиль кулачка. (Если расстояние между точками В получается большим, то можно на кривой перемещений найти промежуточное значение
соединяем плавной кривой, которая представляет собой центровой (теоретический) профиль кулачка. (Если расстояние между точками В получается большим, то можно на кривой перемещений найти промежуточное значение  , по которому построим дополнительное положение точки В). На теоретическом профиле выбираем точки (12 или более), из которых проводим окружности радиусом
, по которому построим дополнительное положение точки В). На теоретическом профиле выбираем точки (12 или более), из которых проводим окружности радиусом  мм. С внутренней стороны ко всем окружностям проводим общую кривую касательную линию, которая служит рабочим (действительным) профилем кулачка. Действительный профиль кулачка и ролик с толкателем в одном из положений обводим толстыми линиями, а остальные построения – тонкими.
мм. С внутренней стороны ко всем окружностям проводим общую кривую касательную линию, которая служит рабочим (действительным) профилем кулачка. Действительный профиль кулачка и ролик с толкателем в одном из положений обводим толстыми линиями, а остальные построения – тонкими.
Для оценки точности построений найдем величину скорости толкателя в одном из положений, например, в третьем. Для этого замеряем длину ординаты (рис 4.1) в положении 3, которая в данном случае равна  . Тогда скорость толкателя будет иметь значение
. Тогда скорость толкателя будет иметь значение
 .
.
Построим план скоростей для того же положения, используя векторное уравнение 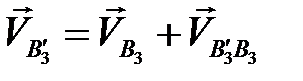 .
.
Здесь 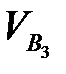 – скорость точки
– скорость точки  , принадлежащей кулачку,
, принадлежащей кулачку,
 – скорость точки
– скорость точки  , принадлежащей толкателю.
, принадлежащей толкателю.
Находим скорость 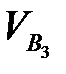
 ,
,
где  – действительная величина радиуса кулачка в положении 3.
– действительная величина радиуса кулачка в положении 3.
Значение  находится путем замера расстояния
находится путем замера расстояния  и умножения его на
и умножения его на  ,
,  .
.
Следовательно,  .
.
Выбираем масштабный коэффициент 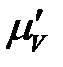 для построения плана скоростей, изображая скорость
для построения плана скоростей, изображая скорость 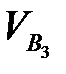 произвольным отрезком
произвольным отрезком  (рис. 4.4)
(рис. 4.4)
 .
.
Из полюса  проводим вектор
проводим вектор  , перпендикулярный
, перпендикулярный  , в сторону вращения кулачка. В точке
, в сторону вращения кулачка. В точке  теоретического профиля проводим касательную
теоретического профиля проводим касательную  , которую переносим в точку
, которую переносим в точку  на плане скоростей. Из полюса
на плане скоростей. Из полюса 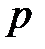 проводим линию, параллельную толкателю в данном положении. На пересечении ставим стрелки и букву
проводим линию, параллельную толкателю в данном положении. На пересечении ставим стрелки и букву  , получая векторы
, получая векторы  и
и  . Замеряем длину вектора
. Замеряем длину вектора  , умножаем на
, умножаем на  , получая скорость толкателя
, получая скорость толкателя
 .
.
Расчеты показали, что величины скоростей толкателя, найденные двумя способами, практически совпадают, что свидетельствует о высокой точности построений.
Дата добавления: 2015-02-10; просмотров: 301; Мы поможем в написании вашей работы!; Нарушение авторских прав |