Кривошипно-ползунный механизм

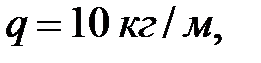
Известны следующие параметры механизма (рис. 3.1): (Все ускорения берутся из первого листа курсового проекта).

Требуется определить реакции в кинематических парах и уравновешивающую силу.

Изображаем механизм в заданном положении с обозначением масштабного коэффициента м/мм, который в данном случае обозначает, что механизм уменьшен в два раза. На механизм действуют следующие силы.

1.Сила полезного сопротивления 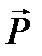, указываемая в задании. Она приложена в точке В ползуна 3 и направлена горизонтально.

2.Силы тяжести 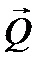, определяемые через массы звеньев, которые можно условно найти по формуле 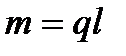, где q –масса единицы длины звена, l –длина звена

Следовательно,

Силы тяжести прикладываются в центрах масс S₁, S₂, S₃ и направлены вертикально вниз.

3.Силы инерции звеньев 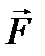, определяемые по формуле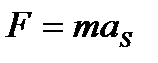

Эти силы прикладываются в центрах масс и направлены они в стороны, обратные ускорениям . (Желательно план ускорений с первого листа перенести на второй лист).

4.Момнеты сил инерции М, которые можно найти по формуле 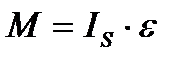, где I_S –моменты инерции звеньев относительно центральных осей

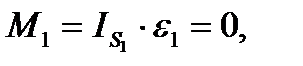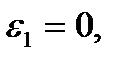
т.к.

т.к.

Моменты инерции звеньев определяем по формуле

.

Следовательно,

Моменты сил инерции М направлены в стороны, обратные угловым ускорениям.

5. Уравновешивающая сила , прикладываемая в точке А кривошипа 1 и направленная перпендикулярно ему. Пусть в нашем примере она направлена вверх.

Все силы и моменты указываем на механизме, причем длины векторов берем произвольно.

Изображаем отдельно структурную группу, состоящую из шатуна 2 и ползуна 3 (рис. 3.2). Реакцию 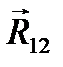направляем пока произвольно, а реакцию вертикально. Пусть она направлена вниз. Рассматриваем равновесие группы и записываем уравнение моментов относительно точки А. Для этого сначала из точки А проводим перпендикуляры ко всем силам, замеряем их длины в миллиметрах и умножаем на 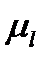, получая их величины:

Уравнение равновесия будет иметь вид:

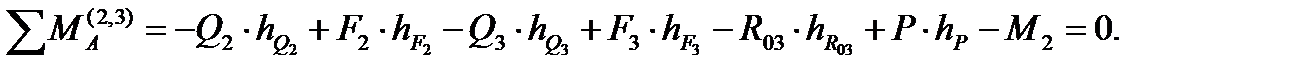
Откуда

Так как эта сила оказалась отрицательной, то вектор мы зачеркиваем (стирать нельзя!) и направляем в другую сторону.

Используя графическое условие равновесия группы , составляем силовой многоугольник (рис. 3.3) в масштабе .

Вычисляем длины векторов сил

Силы в многоугольнике идут в любом порядке, но желательно, чтобы сначала шли все силы одного звена, а затем силы, действующие на другое звено. Если длина вектора силы окажется менее 3 мм, то вместо этой силы ставим точку, около которой записываем обозначение силы. Начало первой силы (в данном случае это сила ) обозначаем точкой. Соединяем конец последней силы (у нас это ) с началом первой, получая вектор 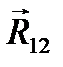, который направлен в начало силы . Замеряем длину этого вектора в миллиметрах и умножаем на 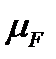, получая величину силы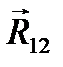

Вектор 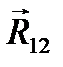в точке А перечеркиваем и направляем его так, как он идет в многоугольнике.

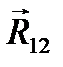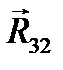Чтобы получить реакцию в шарнире В, нужно рассмотреть равновесие одного звена, например, второго. Для этого начало силы нужно соединить с концом силы . Получаем вектор , который идет в начало силы 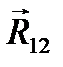. Замеряем длину этого вектора и умножаем на 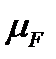, получая значение силы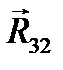

Изображаем отдельно кривошип 1 со всеми силами (рис. 3.4.), причем реакцию 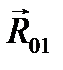направляем пока произвольно, а сила 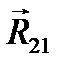направлена в сторону, обратную силе 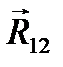, т.е. 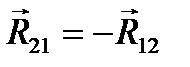.Из точки О проводим перпендикуляры ко всем силам, замеряем их и умножаем на 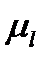. Получаем длины плеч сил.

Рассматривая равновесие кривошипа, записываем уравнение моментов относительно точки О

Откуда

Используем графическое условие равновесия кривошипа , строим силовой многоугольник в масштабе (рис. 3.5).

Находим длины векторов

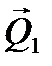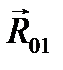Соединяя начало первой силы и конец последней , получаем вектор , который направлен в начало силы 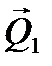. Находим величину этой силы

Вектор 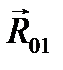в точке О перечеркиваем и направляем так, как он идет в многоугольнике.

Для поверки точности расчетов и построений найдем уравновешивающую силу по методу Жуковского. Момент силы инерции второго звена заменяем парой сил и (рис 3.1), действующих, например, в точках А и С и направленных перпендикулярно шатуну АС. При этом направление пары сил должно совпадать с направлением момента .

Найдем величины этих сил

Переносим с первого листа курсовой работы план скоростей, на который помещаем все внешние силы (рис. 3.6), приложив их в соответствующие точки и повернув на 90˚ в ту или иную сторону. В нашем случае все силы повернуты по часовой стрелке. Из полюса скоростей р проводим к силам перпендикуляры, которые являются плечами сил. Замеряем длины перпендикуляров и записываем уравнение моментов относительно полюса р

Откуда

Сравнение результатов, полученных двумя способами, говорит о том, что погрешность вычислений и построений незначительна.