
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Векторы
Физические величины можно разделить на два типа: скалярные и векторные. Скалярные величины (масса, длина, работа, энергия, электрический заряд и др.) полностью характеризуются одним числовым значением. Скалярные величины в свою очередь тоже подразделяют на два вида: истинные скаляры, которые всегда являются положительными величинами (например, масса, длина, кинети-ческая энергия и др.), и алгебраические величины, которые могут принимать поло-жительные и отрицательные значения (например, заряд, потенциальная энергия, работа). Векторные величины (перемещение, скорость, ускорение, сила, импульс, момент силы, напряженность электрического поля, магнитная индукция и др.) характеризуются не только числовым значением, но и направлением в прост-ранстве. Числовое значение вектора называется модулем и характеризует длину вектора. Геометрический образ вектора – это направленный отрезок прямой.
Существование такого разделения объективно обусловлено. Так, заданная масса тела (скаляр!) полностью характеризует его инерционные и гравитационные свойства, в то время как известный модуль перемещения (вектора!) позволяет найти лишь расстояние, на котором будет находиться тело от точки начала движения, но не позволяет найти точку, где это тело будет находиться.
Векторы характеризуются модулем и ортом вектора. Важнейшим понятием векторной алгебры является понятие проекции вектора на ось.
Над векторами можно выполнить пять алгебраических действий: сложение, вычитание, умножение вектора на число, скалярное произведение, векторное произведение (обратите внимание на отличие этих действий от четырех арифметических действий). Определения, основные характеристики векторов и действия над векторами подробно изложены в прил. 1 и 2.
Вопросы для самопроверки и задачи
1) Для чего нужны векторные величины?
2) Сформулируйте определение векторной величины.
3) Какие алгебраические действия можно выполнять с векторами?
4) Что такое орт вектора, модуль вектора, как их вычислить?
5) Что такое проекция вектора на ось, от чего зависит ее знак?
Задача 1. (1) Выбрать правильные и ошибочные записи: 1)  2)
2)  3)
3)  4)
4)  5)
5) 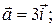 6)
6)  7)
7)  8)
8)  9)
9)  10)
10) 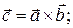 11)
11)  12)
12)  13)
13)  14)
14)  15)
15) 
Задача 2. (1) Небольшой камень падает вниз, двигаясь с ускорением свободного падения, и достигает в некоторый момент времени скорость, равную 13 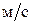 . Чему равны в этот момент времени проекции ускорения и скорости на ось: 1) Ox1, направленную горизонтально вправо; 2) Ox2, направленную горизонтально влево; 3) Oy1, направленную вертикально вверх; 4) Oy2, направленную вертикально вниз.
. Чему равны в этот момент времени проекции ускорения и скорости на ось: 1) Ox1, направленную горизонтально вправо; 2) Ox2, направленную горизонтально влево; 3) Oy1, направленную вертикально вверх; 4) Oy2, направленную вертикально вниз.
Задача 3. (1) Автомобиль движется по прямому горизонтальному участку шоссе с ускорением, равным 1,2  и развивает к некоторому моменту времени скорость, равную 28
и развивает к некоторому моменту времени скорость, равную 28 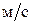 .Чему равны в этот момент времени проекции ускорения и скорости на ось: 1) Ox1, направленную вдоль дороги по ходу автомобиля; 2) Ox2, направленную вдоль дороги против хода автомобиля; 3) Oy1, направленную вертикально вверх; 4) Oy2, направленную вертикально вниз.
.Чему равны в этот момент времени проекции ускорения и скорости на ось: 1) Ox1, направленную вдоль дороги по ходу автомобиля; 2) Ox2, направленную вдоль дороги против хода автомобиля; 3) Oy1, направленную вертикально вверх; 4) Oy2, направленную вертикально вниз.
Задача 4. (1) Турист движется со скоростью 1,6 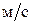 на северо-восток, ориентируясь по компасу. Угол между направлением его скорости и направлением на восток равен 30°. Найти проекции скорости движения туриста на координатные оси, направленные с запада на восток и с юга на север.
на северо-восток, ориентируясь по компасу. Угол между направлением его скорости и направлением на восток равен 30°. Найти проекции скорости движения туриста на координатные оси, направленные с запада на восток и с юга на север.
Задача 5. (1) Самолет, подлетая к взлетно-посадочной полосе, движется по глиссаде, имея скорость 400  , направленную, очевидно, «вперед и вниз» под углом 10° к горизонту. Ось Ox направлена вдоль полосы по ходу самолета, а ось Oy – вертикально вверх. Выполнить рисунок и найти проекции скорости самолета на эти оси. Как необходимо направить оси координат, чтобы в некоторый момент времени лишь одна из проекций была отлична от нуля?
, направленную, очевидно, «вперед и вниз» под углом 10° к горизонту. Ось Ox направлена вдоль полосы по ходу самолета, а ось Oy – вертикально вверх. Выполнить рисунок и найти проекции скорости самолета на эти оси. Как необходимо направить оси координат, чтобы в некоторый момент времени лишь одна из проекций была отлична от нуля?
Задача 6. (2) На сани, которые тянет мальчик за веревку, образующую с горизонтом угол 30°, действуют четыре силы: сила натяжения нити, направленная вдоль нити; сила тяжести, направленная вниз; сила реакции опоры, направленная вверх; сила трения, направленная против движения. Найти проекции этих сил на горизонтальную и вертикальную координатные оси.
Задача 7. (2) На лыжника, спускающегося с горы, наклон которой к горизонту составляет 30°, действуют три силы: сила тяжести, направленная вертикально вниз; сила реакции опоры, направленная перпендикулярно поверхности горы вверх; сила трения, направленная против направления движения лыжника. Найти проекции этих векторов на ось Ox, направленную вдоль наклонной плоскости вниз, и на ось Oy, направленную перпендикулярно поверхности горы вверх.
Задача 8. (1 – 3) Для векторов  , заданных проекциями на декартовы оси, записать их разложение по осям координат, найти их модуль, сумму, разность, скалярное и векторное произведение:
, заданных проекциями на декартовы оси, записать их разложение по осям координат, найти их модуль, сумму, разность, скалярное и векторное произведение:
а)  = (3,5; 5,2; –7,4),
= (3,5; 5,2; –7,4), 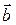 = (–1,7; 2,3; 4,3);
= (–1,7; 2,3; 4,3);
б)  = (8,2; 5,6; 4,9),
= (8,2; 5,6; 4,9), 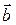 = (3,4; 2,8; –2,5);
= (3,4; 2,8; –2,5);
в)  = (0; 4,8; 4,3),
= (0; 4,8; 4,3), 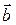 = (2,4; 3,1; 0);
= (2,4; 3,1; 0);
г)  = (2,5; 0; –4,2),
= (2,5; 0; –4,2), 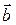 = (–3,6; 0; 2,8).
= (–3,6; 0; 2,8).
Задача 9. (2) Найти проекцию вектора  = (1,7; 2,3; 4,4) на ось, орт которой равен орту вектора
= (1,7; 2,3; 4,4) на ось, орт которой равен орту вектора 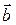 = (4,1; 1,3; 2,2).
= (4,1; 1,3; 2,2).
Задача 10. (2) Найти орт нормали к плоскости, в которой лежат векторы  = (6,3; 5,2; 4,8) и
= (6,3; 5,2; 4,8) и 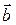 = (3,1; 4,3; 5,2).
= (3,1; 4,3; 5,2).
Задача 11.(1) Чему равен угол между векторами  = (3,3; 4,2; 4,6) и
= (3,3; 4,2; 4,6) и 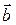 = (6,1; 2,3; 1,2).
= (6,1; 2,3; 1,2).
Задача 12. (2) Найти проекцию орта вектора  = (1,4; 4,7; 3,2) на ось Ox.
= (1,4; 4,7; 3,2) на ось Ox.
Задача 13. (2) Найти орт вектора  = (2,7; 3,8; –1,3) и убедиться в том, что его длина равна единице.
= (2,7; 3,8; –1,3) и убедиться в том, что его длина равна единице.
Задача 14. (2) Получить выражение для вычисления скалярного произведения векторов, представленных в виде разложения по осям декартовой системы координат.
Задача 15. (3) Получить выражения для вычисления векторного произведения векторов, представленных в виде разложения по осям декартовой системы координат.
Задача 16. (2) Доказать, что скалярное произведение не изменится при перемене мест сомножителей, т. е. что  .
.
Задача 17. (3) Доказать, что векторное произведение меняет знак при перемене мест сомножителей, т. е. что 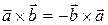 .
.
Дата добавления: 2015-04-15; просмотров: 285; Мы поможем в написании вашей работы!; Нарушение авторских прав |