Действия над векторами

Рис. П.2.1 Рис. П.2.2   Рис. П.2.3

Сложение векторов: выполняется по правилу треугольника или параллелограмма. При сложении векторов по правилу треугольника (рис. П.2.1) длина результирующего вектора может быть рассчитана по теореме косинусов: . При сложении векторов по правилу параллелограмма (рис. П.2.2) из теоремы косинусов легко получить выражение для вычисления длины результирующего вектора: . Умножение вектора на число (рис. П.2.3) изменяет только длину вектора, если число положительное, а при отрицательном числе изменяет еще и нап-равление вектора на противоположное: .

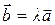Вычитание векторов с учетом действия (П.2.4) сводится к сложению вектора с вектором, противоположным вектору :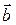

.

Скалярное произведение векторов определяется выражением:

,

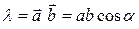где α – угол между векторами и .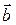

Векторное произведение векторов можно записать так:

,

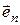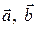где – орт нормали к плоскости (часто ), в которой лежат векторы , направленный так, что векторы образуют правовинтовую тройку векторов, т. е. при вращении правого винта в нап-равлении от первого вектора ко второму (от к ) винт должен двигаться поступательно в сторону третьего ( ) вектора (рис. П.2.4). Рассмотрим характеристики вектора. Используя правило умножения вектора на число, произвольный вектор (рис. П.2.5) можно представить в виде: 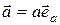, где a – длина (модуль); – орт вектора . Проекция вектора на ось (рис. П.2.6) определяется формулой: , где α – угол между вектором и осью x (0 ≤ α ≤ π).

Рис. П.2.4 Рис. П.2.5   Рис. П.2.6

Вектор можно разложить по трем взаимно перпендикулярным направлениям в пространстве, например по трем декартовым осям координат. Выбрав единичные векторы (орты) (иногда обозначаются как ) вдоль осей Ox, Oy и Oz, любой вектор можно представить в виде:

,

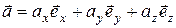где – проекции вектора на оси декартовой системы координат.

Тогда модуль вектора рассчитывается по формуле:

.

Формула позволяет выполнять действия над векторами аналитически, без геометрического сложения на рисунке, что особенно удобно в том случае, если векторы изменяются с течением времени.

ПРИЛОЖЕНИЕ 3

Правила дифференцирования и таблица производных

Из определения производной вытекают несколько правил дифференцирования, использование которых позволяет свести дифференцирование функций к вычислению производных элементарных функций:

производная постоянной величины (константы) равна нулю:

;

постоянная величина (константа), являющаяся сомножителем функции, при дифференцировании выносится за знак производной:

;

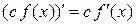производная суммы (разности) функций равна сумме (разности) производных функций:

;

производная произведения двух функций равна производной первой функции, умноженной на вторую, плюс произведение первой функции на производную второй:

;

производная частного при делении двух функций преобразовывается по формуле:

;

производная сложной функции (т. е. функции от функции) равна произведению производной внешней функции по всему ее аргументу (т. е. по вложенной функции g) и производной вложенной функции по ее аргументу:

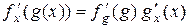
или

.

(Производная сложной функции – наиболее сложное для практического применения правило дифференцирования, поэтому приведены две формы записи этого правила.)

Расчет погрешности косвенных измерений при выполнении лабораторных работ требует умения вычислять частные производные функции многих переменных. Чтобы вычислить такую производную по одному из аргументов, необходимо все остальные переменные объявить константами и руководствоваться далее обычными правилами дифференцирования:

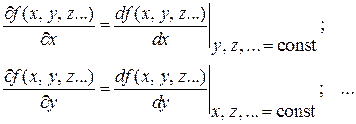
Производные некоторых наиболее часто встречающихся элементарных функций:

гармонических функций синуса и косинуса:

; (П.3.9а) ;

экспоненциальной и логарифмической функций:

; (П.3.10а) ;

степенной функции и два ее частных случая для n = –1 и n = соответственно:

; (П.3.11а) ; (П.3.11б) .

(Более полную таблицу производных можно найти в учебниках по высшей математике, либо в специальных справочниках.)

ПРИЛОЖЕНИЕ 4

Правила интегрирования и таблица интегралов

Неопределенный интеграл функции f(x) равен сумме первообразной F(x) этой функции и произвольной постоянной (константы):

.

Напомним, что первообразная F(х) функции f(x) это такая функция, производная от которой равна f(x), т. е. . Операции дифференцирования и интегрирования – две противоположные операции (напоминают противоположные друг другу алгебраические действия возведения в степень и извлечения корня).

Из определения интеграла вытекают несколько правил интегрирования, которые позволяют значительно упростить вычисление интегралов:

интеграл от дифференциала переменной (или функции) равен сумме самой переменной (или функции) и постоянной величины (константы):

;

интеграл суммы (разности) функций равен сумме (разности) интегралов:

;

постоянный сомножитель можно вынести за знак интеграла:

;

правило интегрирования по частям:

.

Кроме неопределенного интеграла, который представляет собой функцию, по формуле Ньютона-Лейбница можно вычислить определенный интеграл:

.

Интегралы некоторых, наиболее часто встречающихся элементарных функций:

от тригонометрических функций синуса и косинуса –

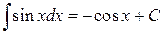; (П.4.7а) ;

от экспоненциальной и логарифмической функций –

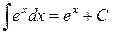; (П.4.8а) ;

от степенной функции –

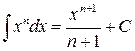(при ); (П.4.9а) .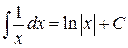

(Более полную таблицу интегралов можно найти в учебниках по высшей математике, либо в специальных справочниках.)

Некоторые физические задачи приводят к дифференциальным уравнениям. Решить дифференциальное уравнение – значит найти функцию (или функции), которая бы обращала уравнение в тождество. Наиболее простой вид дифференциальных уравнений – это уравнения с разделяющимися переменными:

или

.

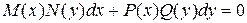Для решения уравнения с разделяющимися переменными необходимо обе его части умножить или разделить на такое выражение, чтобы в одну часть уравнения входили только x, в другую – только y, и затем проинтегрировать обе части. Появившуюся в решении постоянную интегрирования можно определить из начальных или граничных условий.

ПРИЛОЖЕНИЕ 5