Движение с постоянным ускорением

Положение тел относительно выбранной системы координат принято характеризовать радиусом-вектором 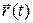, зависящим от времени. Тогда положение тела в пространстве в любой момент времени можно найти по формуле:

.

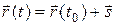(Напомним, что в этом и заключается основная задача механики.)

Среди множества различных видов движения самым простым является равномерное – движение с постоянной скоростью (нулевым ускорением), причем неизменным должен оставаться вектор скорости ( 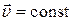). Очевидно, что такое движение может быть только прямолинейным. Именно при равномерном движении перемещение вычисляется по формуле:

.

Иногда тело движется по криволинейной траектории так, что модуль скорости остается постоянным ( 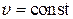) (такое движение нельзя назвать равномерным и к нему нельзя применить формулу ). В этом случае пройденный путь может быть вычислен по простой формуле:

.

Примером такого движения является движение по окружности с постоянной по модулю скоростью.

Более сложным является равноускоренное движение – движение с постоянным ускорением ( ). Для такого движения справедливы две формулы кинематики:

;

,

из которых можно получить две дополнительные формулы, которые часто могут быть полезны при решении задач:

;

.

Равноускоренное движение не обязательно должно быть прямолинейным. Необходимо лишь, чтобы вектор ускорения оставался постоянным. Примером равноускоренного, но не всегда прямолинейного движения, является движение с ускорением свободного падения (g = 9,81 м/с²), направленным вертикально вниз.

Из школьного курса физики знакомо и более сложное движение – гармонические колебания маятника, для которого формулы – не справедливы.

При движении тела по окружности с постоянной по модулю скоростью оно движется с так называемым нормальным (центростремительным) ускорением

,

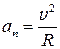направленным к центру окружности и перпендикулярным скорости движения.

В более общем случае движения по криволинейной траектории с меняющейся скоростью ускорение тела можно разложить на две взаимно перпендикулярные составляющие и представить в виде суммы тангенциального (касательного) 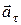и нормального (перпендикулярного, центростремительного) ускорения:

,

где – орт вектора скорости и орт нормали к траектории; R – радиус кривизны траектории.

Движение тел всегда описывается относительно какой-либо системы отсчета (СО). При решении задач необходимо выбрать наиболее удобную СО. Для поступательно движущихся СО формула

позволяет легко переходить от одной СО к другой. В формуле – скорость тела относительно одной СО; – скорость тела относительно второй СО; – скорость второй СО относительно первой.

Вопросы для самопроверки и задачи

1) Модель материальной точки: в чем ее суть и смысл?

2) Сформулируйте определение равномерного, равноускоренного движения.

3) Сформулируйте определения основных кинематических величин (радиуса-вектора, перемещения, скорости, ускорения, тангенциального и нормального ускорения).

4) Напишите формулы кинематики равноускоренного движения, выведите их.

5) Сформулируйте принцип относительности Галилея.

2.1.1. Прямолинейное движение

Задача 22.(1) Автомобиль движется по прямолинейному участку дороги с постоянной скоростью 90 . Найти перемещение автомобиля за 3,3 мин и его положение в этот же момент времени, если в начальный момент времени автомобиль находился в точке, координата которой равна 12,23 км, а ось Ox направлена 1) вдоль движения автомобиля; 2) против движения автомобиля.

Задача 23.(1) Велосипедист движется по загородной дороге на север со скоростью 12 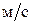в течение 8,5 мин, затем он, свернув направо на перекрестке, проехал еще 4,5 км. Найти перемещение велосипедиста за время его движения.

Задача 24.(1) Конькобежец движется прямолинейно с ускорением 2,6 , и за 5,3 с его скорость увеличилась до 18 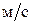. Найти начальное значение скорости конькобежца. Какое расстояние пробежит спортсмен за это время?

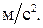Задача 25.(1) Автомобиль движется прямолинейно, притормаживая перед знаком ограничения скорости 40 с ускорением 2,3 Сколько времени длилось такое движение, если перед началом торможения скорость автомобиля была равна 70 ? На каком расстоянии от знака водитель начал тормозить?

Задача 26.(1) С каким ускорением движется поезд, если на пути 1200 м его скорость возросла от 10 до 20 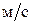? Сколько времени затратил поезд на этот путь?

Задача 27. (1) Тело, брошенное вертикально вверх, вернулось на землю через 3 с. Какова была начальная скорость тела? На какой максимальной высоте оно побывало?

Задача 28.(2) Тело на веревке поднимают с поверхности земли с ускорением 2,7 м/с² вертикально вверх из состояния покоя. Через 5,8 с веревка оборвалась. Сколько времени двигалось тело до земли после того, как оборвалась веревка? Сопротивлением воздуха пренебречь.

Задача 29. (2) Тело начинает двигаться без начальной скорости с ускорением 2,4 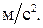Определить путь, пройденный телом за первые 16 с от начала движения, и путь, пройденный за последующие 16 с. С какой средней скоростью двигалось тело эти 32 с?

2.1.2. Равноускоренное движение в плоскости

Задача 30. (1) Баскетболист бросает мяч в кольцо со скоростью 8,5 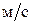под углом 63^о к горизонту. С какой скоростью мяч попал в кольцо, если долетел до него за 0,93 с?

Задача 31. (1) Баскетболист бросает мяч в кольцо. В момент броска мяч находится на высоте 2,05 м, а через 0,88 с падает в кольцо, расположенное на высоте 3,05 м. С какого расстояния от кольца (по горизонтали) произведен бросок, если мяч был брошен под углом 56^о к горизонту?

Задача 32.(2) Мяч брошен горизонтально со скоростью 13 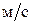, спустя некоторое время его скорость оказалась равной 18 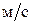. Найти перемещение мяча за это время. Сопротивлением воздуха пренебречь.

Задача 33. (2) Тело брошено под некоторым углом к горизонту с начальной скоростью 17 м/с. Найти величину этого угла, если дальность полета тела в 4,3 раза больше максимальной высоты подъема.

Задача 34. (2) Бомбардировщик, пикирующий со скоростью 360 км/ч, сбрасывает бомбу с высоты 430 м, находясь по горизонтали на расстоянии 250 м от цели. Под каким углом должен пикировать бомбардировщик? На какой высоте окажется бомба спустя 2 с от начала падения? Какую скорость она будет иметь в этой точке?

Задача 35. (2) Самолет, летевший на высоте 2940 м со скоростью 410 км/ч, сбросил бомбу. За какое время до прохождения над целью и на каком расстоянии от нее самолет должен сбросить бомбу, чтобы попасть в цель? Найти модуль и направление скорости бомбы спустя 8,5 с от начала ее падения. Сопротивлением воздуха пренебречь.

Задача 36. (2) Снаряд, выпущенный под углом 36,6^о к горизонту, дважды был на одной и той же высоте: спустя 13 и 66 с после вылета. Определить начальную скорость, максимальную высоту подъема и дальность полета снаряда. Сопротивлением воздуха пренебречь.

2.1.3. Движение по окружности

Задача 37. (2) Грузило, движущееся на леске по окружности с постоянным тангенциальным ускорением, к концу восьмого оборота имело скорость 6,4 м/с, а после 30 с движения его нормальное ускорение стало 92 м/с². Найти радиус этой окружности.

Задача 38. (2) Мальчик, катающийся на карусели, движется при остановке карусели по окружности радиусом 9,5 м и проходит путь 8,8 м, имея в начале этой дуги скорость 3,6 м/с, а в конце – 1,4 м/с. Определить полное ускорение мальчика в начале и конце дуги, а также время его движения по этой дуге.

Задача 39. (2) Муха, сидящая на краю лопасти вентилятора, при его включении движется по окружности радиусом 32 см с постоянным тангенциальным ускорением 4,6 см/с². Через сколько времени после начала движения нормальное ускорение будет вдвое больше тангенциального и чему будет равна линейная скорость мухи в этот момент времени? Сколько оборотов муха сделает за это время?

Задача 40. (2) При открывании двери ручка из состояния покоя движется по окружности радиусом 68 см с постоянным тангенциальным ускорением, равным 0,32 м/с². Найти зависимость полного ускорения ручки от времени.

Задача 41. (3) Для экономии места въезд на один из высочайших в Японии мостов устроен в виде винтовой линии, обвивающей цилиндр радиусом 65 м. Полотно дороги составляет с горизонтальной плоскостью угол 4,8^о. Найти ускорение автомобиля, движущегося по этой дороге с постоянной по модулю скоростью, равной 85 км/ч?

2.1.4. Относительность движения

Задача 42.(2) Два корабля движутся относительно берегов со скоростью 9,00 и 12,0 узлов (1 узел = 0,514 м/с), направленной под углом 30 и 60^о к меридиану соответственно. С какой скоростью второй корабль движется относительно первого?

Задача 43. (3) Мальчик, который может плавать со скоростью, в 2,5 раза меньшей скорости течения реки, хочет переплыть эту реку так, чтобы его как можно меньше снесло вниз по течению. Под каким углом к берегу мальчик должен плыть? На какое расстояние его снесет, если ширина реки равна 190 м.

Задача 44. (3) Два тела одновременно начинают двигаться из одной точки в поле силы тяжести с одинаковой скоростью, равной 2,6 м/с. Скорость одного тела направлена под углом π/4, а другого – под углом –π/4 к горизонту. Определить относительную скорость этих тел через 2,9 с после начала их движения.