
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Аналогично, рассматривая формулу определения скорости в общем случае

как дифференциальное уравнение с разделяющимися переменными, положение тела в пространстве можно найти после интегрирования:
 .
.
Путь, пройденный телом за промежуток времени (Δt = t – t0), можно вычислить как интеграл от модуля скорости:
 .
.
Радиус-вектор, как и любой другой вектор, можно выразить через проекции и орты выбранной системы координат. Формула
 ;
;
представляет радиус-вектор в декартовой системе координат.
Система функций

является уравнением траектории в параметрической форме, где параметром является время t. Если движение происходит в одной плоскости, например xOy, то можно получить уравнение траектории в явном виде:  , для чего нужно из первых двух функций системы исключить время.
, для чего нужно из первых двух функций системы исключить время.
Вопросы для самопроверки и задачи
1) Выведите формулы зависимости скорости и перемещения от времени, если известна зависимость ускорения от времени.
2) Выведите уравнение траектории движения тела, брошенного под углом к горизонту.
3) Запишите радиус-вектор в виде разложения по базису декартовой системы координат.
4) Выведите формулы для нахождения скорости и ускорения тела в декартовой системе координат.
2.2.1. Обратная задача механики
Задача 45. (1, 2) Найти размерность постоянных А, В и С; радиус-вектор в момент времени, равный 2,6 с, и изобразить его на рисунке; перемещение за промежуток времени от t1 = 0,73 с до t2 = 2,3 с; его модуль; написать уравнение траектории, если частица движется таким образом, что ее радиус-вектор меняется с течением времени по закону:
а)  ; б)
; б) 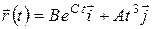 ;
;
в) 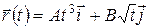 ; г)
; г) 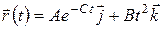 ;
;
д)  ; е)
; е) 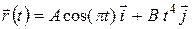 ,
,
где А = 1,8; В = 4,3; С = 1,7 – постоянные коэффициенты.
Задача 46. (2) Реактивный снаряд движется в плоскости yOz так, что его координаты меняются с течением времени по закону: 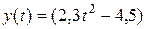 м;
м;  м. Найти уравнение траектории и тангенциальное ускорение снаряда
м. Найти уравнение траектории и тангенциальное ускорение снаряда 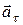 в момент времени, равный 86 с.
в момент времени, равный 86 с.
Задача 47. (2) Движение бегуна на стадионе задано формулами:  ;
; 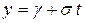 , где α = 4,3 м; β = 2,4 м/с2; γ = 3,1 м; σ = 5,2 м/с. Найти: 1) скорость спортсмена в тот момент, когда его координата х равна 4,7 м; 2) зависимость ускорения спортсмена от времени.
, где α = 4,3 м; β = 2,4 м/с2; γ = 3,1 м; σ = 5,2 м/с. Найти: 1) скорость спортсмена в тот момент, когда его координата х равна 4,7 м; 2) зависимость ускорения спортсмена от времени.
Задача 48. (3) Голубь перемещается в пространстве так, что его радиус-вектор меняется с течением времени по закону:  , где А = 0,53 м/с2; В = 0,32 м/с2; С = 2,8 м. Найти: 1) путь, который пролетела птица за 16 с от начала полета; 2) модуль мгновенного ускорения в момент времени, равный 0,85 с.
, где А = 0,53 м/с2; В = 0,32 м/с2; С = 2,8 м. Найти: 1) путь, который пролетела птица за 16 с от начала полета; 2) модуль мгновенного ускорения в момент времени, равный 0,85 с.
Задача 49. (3) Зависимость координат модели гоночного автомобиля от времени имеет вид:  , где А = 5,6 м; ω = 2,1 рад/с. Определить зависимость модуля нормального и тангенциального ускорения от времени, а также путь, пройденный моделью за 73 с.
, где А = 5,6 м; ω = 2,1 рад/с. Определить зависимость модуля нормального и тангенциального ускорения от времени, а также путь, пройденный моделью за 73 с.
Задача 50. (3) Снаряды вылетают с начальной скоростью 550 м/с под углом 30, 45 и 60о к горизонту. Определить радиус кривизны траектории снарядов в их наивысшей и начальной точках.
Задача 51. (3) С вышки высотой 14,7 м в горизонтальном направлении брошен камень с начальной скоростью 12 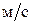 . Определить скорость, тангенциальное и нормальное ускорение камня спустя 0,83 с после начала его движения. Чему равны радиус кривизны и расстояние до земли в этой точке траектории? Сопротивлением воздуха пренебречь.
. Определить скорость, тангенциальное и нормальное ускорение камня спустя 0,83 с после начала его движения. Чему равны радиус кривизны и расстояние до земли в этой точке траектории? Сопротивлением воздуха пренебречь.
2.2.2. Прямая задача механики
Задача 52. (2, 3) Найти размерность постоянных А, В, С, D и зависимость вектора перемещения материальной точки от времени, если материальная точка движется таким образом, что вектор ее скорости меняется с течением времени по закону:
а)  ; б)
; б) 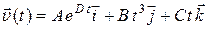 ;
;
в)  ; г)
; г) 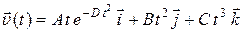 ;
;
д)  ; е)
; е)  .
.
Задача 53. (3) Частица движется с зависящим от времени ускорением:  , где А = 2,4 м/с3; В = 7,1 м/с2. Найти в момент времени, равный 2,7 с модуль скорости, модуль радиуса-вектора, а также путь и перемещение частицы за промежуток времени от t1 = 1,4 с до t2 = 3,8 с. В начальный момент времени частица покоилась в начале координат.
, где А = 2,4 м/с3; В = 7,1 м/с2. Найти в момент времени, равный 2,7 с модуль скорости, модуль радиуса-вектора, а также путь и перемещение частицы за промежуток времени от t1 = 1,4 с до t2 = 3,8 с. В начальный момент времени частица покоилась в начале координат.
Задача 54. (2) Скорость стартующего на вираже автомобиля меняется с течением времени по закону:  , где А = 2,4 м/с4; В = 1,6 м/с3. Найти: 1) модуль приращения ускорения за время от t1 = 1,3 с до t2 = 3,2 с; 2) приращение радиуса-вектора за это время. В начальный момент времени автомобиль находился в начале координат.
, где А = 2,4 м/с4; В = 1,6 м/с3. Найти: 1) модуль приращения ускорения за время от t1 = 1,3 с до t2 = 3,2 с; 2) приращение радиуса-вектора за это время. В начальный момент времени автомобиль находился в начале координат.
Задача 55. (2) Скорость зайца меняется с течением времени по закону:  , где α = 2,4 м/с2; β = 5,3 м/с; γ = 3,7 м/с3. Вычислить скорость зайца в момент времени, равный нулю, найти зависимость ускорения и радиуса-вектора зайца от времени.
, где α = 2,4 м/с2; β = 5,3 м/с; γ = 3,7 м/с3. Вычислить скорость зайца в момент времени, равный нулю, найти зависимость ускорения и радиуса-вектора зайца от времени.
Задача 56. (3) Ускорение взлетающего вертолета меняется по закону: 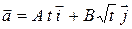 , где А = 3,2 м/с3; В = 4,8 м/с5/2. Вычислить: 1) модуль вектора скорости в момент времени, равный 2,3 с; 2) приращение радиуса-вектора за промежуток времени от t1 = 1,2 с до t2 = 3,6 с. В начальный момент времени вертолет покоился в начале координат.
, где А = 3,2 м/с3; В = 4,8 м/с5/2. Вычислить: 1) модуль вектора скорости в момент времени, равный 2,3 с; 2) приращение радиуса-вектора за промежуток времени от t1 = 1,2 с до t2 = 3,6 с. В начальный момент времени вертолет покоился в начале координат.
Задача 57. (2) Шарик, запрессованный в обод маховика, движется по окружности радиусом 23 см так, что зависимость пути от времени описывается уравнением: l = A + Ct3, где С = 0,52 м/с3. Найти момент времени, когда угол между тангенциальным и полным ускорением шарика будет равен 30о.
Задача 58. (3) Гайка на ободе центрифуги движется по окружности радиусом R. Модуль скорости гайки зависит от пройденного пути по закону: 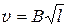 , где В – постоянная. Найти угол между вектором полного ускорения и вектором скорости в зависимости от l.
, где В – постоянная. Найти угол между вектором полного ускорения и вектором скорости в зависимости от l.
3. ДИНАМИКА
Дата добавления: 2015-04-15; просмотров: 339; Мы поможем в написании вашей работы!; Нарушение авторских прав |