
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Координатный способ задания движения
Перейдем от координатного способа задания движения к векторному на основе (2.3). Тогда с учетом (2.6) имеем
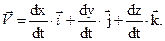
| (2.7) |
Откуда
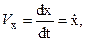
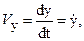

Следовательно проекции скорости на координатные оси определяются первыми производными по времени от соответствующих координат. Модуль скорости
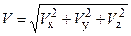 . .
| (2.8) |
Направляющие косинусы вектора скорости относительно координатных осей определяются выражениями (рис. 2.7):
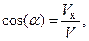
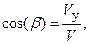

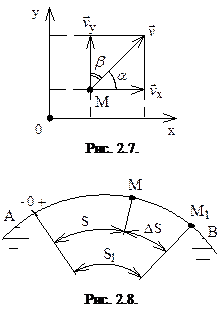 5.3.3. Естественный способ задания движения
5.3.3. Естественный способ задания движения
Дана траектория точки и закон изменения координаты по этой траектории 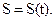
Пусть в момент времени t точка занимала положение М, а в момент времени t1 положение М1 (рис. 2.8).
За время 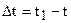 координата получила приращение
координата получила приращение  , тогда
, тогда  то есть средняя скорость равна отношению приращения криволинейной координаты к соответствующему промежутку времени.
то есть средняя скорость равна отношению приращения криволинейной координаты к соответствующему промежутку времени.
Для нахождения истинной скорости перейдем к пределу
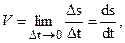 то есть то есть 
| (2.9) |
Численное значение скорости точки при естественном способе задания движения определяется первой производной по времени от криволинейной координаты. Скорость всегда направлена по касательной к траектории точки.
Пример 2.3. Определить скорость точки при t = 1 c, для ее движения по закону 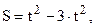 м. На основе (2.9) находим
м. На основе (2.9) находим 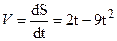 . Для заданного момента времени
. Для заданного момента времени 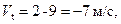 то есть скорость направлена влево (рис. 2.8).
то есть скорость направлена влево (рис. 2.8).
Пример 2.4. Точка M движется в соответствии с уравнениями
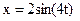 , м; , м; 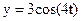 , м. , м.
| (а) |
Определить величину и направление вектора скорости точки и указать ее положение на траектории в момент времени 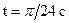 .
.
Решение. Исключая время из уравнений движения, по аналогии с примером 2.1, найдем уравнение траектории
 . .
| (б) |
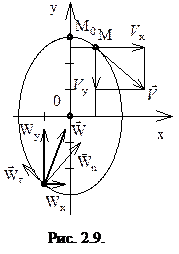 Следовательно, в данном случае точка движется по эллипсу (рис. 2.9). При
Следовательно, в данном случае точка движется по эллипсу (рис. 2.9). При  точка
точка  имела координаты
имела координаты  ;
; 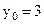 м. В заданный момент времени t координаты точки
м. В заданный момент времени t координаты точки 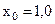 м,
м, 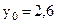 м. Найдем проекции вектора скорости на оси координат:
м. Найдем проекции вектора скорости на оси координат:
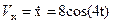 , м/с;
, м/с; 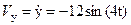 , м/с.
, м/с.
При 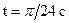 ;
; 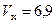 м/c;
м/c; 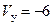 м/c; тогда модуль скорости
м/c; тогда модуль скорости 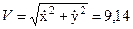 м/с. Направление вектора скорости можно найти по его проекциям на оси координат, или по направляющим косинусам. В частности,
м/с. Направление вектора скорости можно найти по его проекциям на оси координат, или по направляющим косинусам. В частности, 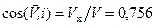 (
( 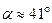 ). Очевидно, при выполнении рисунка в масштабе вектор скорости
). Очевидно, при выполнении рисунка в масштабе вектор скорости  , найденный по его проекциям
, найденный по его проекциям 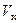 и
и 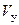 , должен быть направлен по касательной к траектории в точке M.
, должен быть направлен по касательной к траектории в точке M.
Дата добавления: 2015-04-15; просмотров: 239; Мы поможем в написании вашей работы!; Нарушение авторских прав |