
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Уравнения плоского движения
Плоским называют такое движение твердого тела, при котором все его точки описывают плоские траектории, параллельные базовой плоскости.
Уравнения плоского движения можно получить следующим образом. Пусть тело совершает плоское движение по отношению к базовой плоскости (Б.П.) (рис 2.19). Очевидно, все точки, лежащие на перпендикуляре АВ к базовой плоскости, движутся одинаково.
Следовательно, для задания плоского движения твердого тела необходимо и достаточно задать движение какого-нибудь сечения плоскости.
 Как известно, положение плоской фигуры (S) можно задать посредством координат произвольной точки A (полюса) и угла поворота j фигуры относительно полюса (рис. 2.20):
Как известно, положение плоской фигуры (S) можно задать посредством координат произвольной точки A (полюса) и угла поворота j фигуры относительно полюса (рис. 2.20):
  
| (2.29) |
 В качестве полюса можно принять любую точку тела, движение которой известно. Тогда для задания плоского движения тела должны быть заданы три уравнения движения (2.29).
В качестве полюса можно принять любую точку тела, движение которой известно. Тогда для задания плоского движения тела должны быть заданы три уравнения движения (2.29).
При этом первые два уравнения (2.29) описывают поступательную составляющую плоского движения, а третье – вращательную составляющую.
Таким образом, плоское движение сечения (S) (а значит и всего тела) можно рассматривать как состоящее из поступательного вместе с полюсом и вращательного относительно полюса.
Из рассмотрения рисунка 2.21 следует, что при изменении полюса первые два уравнения изменяются, в то время как уравнение для угла поворота не меняется.
Пример 2.9. Определить уравнение плоского движения колеса, которое катится без скольжения прямолинейно (рис. 2.22).
 Будем предполагать, что скорость центра колеса
Будем предполагать, что скорость центра колеса  постоянна, а оси координат в начальном момент времени указаны на чертеже.
постоянна, а оси координат в начальном момент времени указаны на чертеже.
Так как скорость точки C известна, то выберем ее в качестве полюса. В этом случае 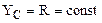 . Для определения
. Для определения  примем во внимание, что
примем во внимание, что  . Тогда
. Тогда  или
или  .
.
Для нахождения функции  учтем, что колесо катится без скольжения, следовательно
учтем, что колесо катится без скольжения, следовательно 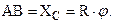 Окончательно уравнения плоского движения колеса в форме (2.29) имеет следующий вид:
Окончательно уравнения плоского движения колеса в форме (2.29) имеет следующий вид:



Дата добавления: 2015-04-15; просмотров: 354; Мы поможем в написании вашей работы!; Нарушение авторских прав |