
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Естественный способ задания движения
Пусть точка движется по криволинейной траектории и в момент времени t имеет скорость V, а в момент времени t1 – скорость V1 (рис. 2.11).
 Перенесем оси естественных координат из положении М в положение М1. В соответствии с (2.11) для определения ускорения необходимо вычислить предел
Перенесем оси естественных координат из положении М в положение М1. В соответствии с (2.11) для определения ускорения необходимо вычислить предел


Спроектируем последнее уравнение на оси естественных координат.
В проекции на ось  получим
получим

При  ,
, 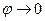 ,
,  ,
,  .
.
Тогда
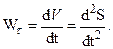
| (2.16) |
Проекция ускорения на касательную, то есть касательное ускорение точки, определяется первой производной по времени от скорости или второй производной по времени от криволинейной координаты S.
Касательное ускорение характеризует изменение вектора скорости по величине. Если  , то ускорение
, то ускорение  .
.
В проекции на ось  получим
получим
 .
.
Для вычисления предела умножим числитель и знаменатель на  .
.

Но 

 где
где  – радиус кривизны траектории. Тогда
– радиус кривизны траектории. Тогда
 . .
| (2.17) |
Таким образом, проекция ускорения на нормаль (нормальное ускорение) определятся отношением квадрата скорости точки к радиусу кривизны траектории.
Нормальное ускорение характеризует изменение вектора скорости по направлению. При прямолинейном движении  .
.
Полное ускорение равно геометрической сумме касательного и нормального ускорений.
 или или  . .
| (2.18) |
Нормальное ускорение направлено по радиусу кривизны к центру кривизны траектории (рис. 2.12).
Пользуясь понятиями касательного и нормального ускорений все многообразие движений точки можно свести к четырем типам, указанным в таблице.
| Wt | Wn | Характер движения |
| = 0 | = 0 | Равномерное прямолинейное |
| ¹ 0 | = 0 | Неравномерное прямолинейное движение |
| = 0 | ¹ 0 | Равномерное криволинейное движение |
| ¹ 0 | ¹ 0 | Неравномерное криволинейное движение. |
Характер изменения скорости точки удобно оценивать по знакам V и Wt.

 Ускоренным называетсятакое движение, при котором модуль скорости увеличивается. Замедленным называется движение точки, при котором модуль скорости уменьшается.
Ускоренным называетсятакое движение, при котором модуль скорости увеличивается. Замедленным называется движение точки, при котором модуль скорости уменьшается.
Пример 2.5. По условию примера 2.4. определить полное, касательное и нормальное ускорения очки М при  с, а также радиус кривизны траектории.
с, а также радиус кривизны траектории.
Решение. В заданный момент времени точка имеет координаты  м,
м,  м (рис. 2.9). Найдем проекции ускорения на оси координат:
м (рис. 2.9). Найдем проекции ускорения на оси координат:
 ;
;  .
.
Для заданного момента времени
 ,
,  ,
,
 ,
,
Для определения касательного и нормального ускорений на основе (2.16) и (2.17) необходимо найти скорость точки М для заданного момента времени:
 ;
;

 .
.
Определение касательного ускорения на основе (2.16) приводит в данном случае к вычислению громоздкой производной  . Эта процедура упростится, если использовать другое, идентичное выражение
. Эта процедура упростится, если использовать другое, идентичное выражение
 , тогда
, тогда
 .
.
Модуль нормального ускорения можно найти на основе (2.18):
 .
.
Правильность вычислений проверяется определением модуля нормального ускорения из выражения

Радиус кривизны траектории в данном положении точки найдем из (2.17):

Направление вектора полного ускорения определяется по его проекциям  и
и  (рис. 2.9). Для проверки правильности построения
(рис. 2.9). Для проверки правильности построения  целесообразно вычислить направляющий косинус
целесообразно вычислить направляющий косинус
 (
(  ).
).
Пример 2.6. В момент выключения двигателей последней ступени баллистическая ракета находилась на высоте H = 640 км и имела скорость 2800 м/с, направленную под углом 15о к горизонту (рис. 2.13).
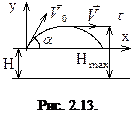 Пренебрегая сопротивлением воздуха, определить максимальную высоту подъема ракеты.
Пренебрегая сопротивлением воздуха, определить максимальную высоту подъема ракеты.
Решение. После выключения двигателя ракета продолжала двигаться с ускорением 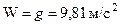 . Для удобства решения поместим начало координат в точку, где находилась ракета в момент выключения двигателя. Найдем проекции ускорения на оси координат.
. Для удобства решения поместим начало координат в точку, где находилась ракета в момент выключения двигателя. Найдем проекции ускорения на оси координат.
 ; ;  . .
| (а) |
Разделим переменные и проинтегрируем уравнения (а):
 ; ;  . .
| (б) |
Постоянные интегрирования найдем по начальным условиям:
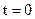 ; ;  , ,  . .
| (в) |
Решая совместно (б) и (в), имеем:
 , ,  . .
| (г) |
Подставим (г) в (б):
 , ,  . .
|
или
 , ,  . .
| (д) |
Разделяя переменные и интегрируя (д) при начальных условиях 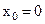 ,
,  , получим:
, получим:
 , ,  . .
| (е) |
Очевидно, Нmax = H+ymax.Максимальное значение ymax имеет место при  ; при этом ограничении можно найти из (д) соответствующее значение времени
; при этом ограничении можно найти из (д) соответствующее значение времени
 . .
| (ж) |
Подставляя (ж) в (е), получим:
 .
.
Таким образом, максимальная высота подъема ракеты составляет Hmax = 640+27 = 667 км.
Дата добавления: 2015-04-15; просмотров: 244; Мы поможем в написании вашей работы!; Нарушение авторских прав |