
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Определение линейных скоростей и ускорений точек вращающегося тела
Для определения скорости и ускорения какой-нибудь точки M вращающегося с угловой скоростью w и угловым ускорением e тела воспользуемся естественным способом задания движения. Так как все точки тела движутся по окружностям (рис. 2.17), то закон движения точки M можно записать в виде

| (2.24) |
 Получив закон движения точки M, найдем ее скорость:
Получив закон движения точки M, найдем ее скорость:
 или
или 
| (2.25) |
Таким образом, для определения скорости точки тела необходимо умножить угловую скорость тела на радиус, то есть расстояние точки до оси вращения. Пользуясь уравнениями (2.16)-(2.18), найдем касательное, нормальное и полное ускорения точки M:
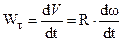 или или 
| (2.26) |
 или или 
| (2.27) |

| (2.28) |
Из анализа уравнений (2.25)-(2.28) следует, что скорость и ускорение любой точки вращающегося тела пропорциональны расстоянию этой точки до оси вращения.
Пример 2.8. Для передачи вращения от электродвигателя к смесителю используется плоскоременная передача, при этом на валу двигателя установлен шкив 1 радиуса R1 = 0,2 м, а на валу смесителя шкив 2 радиуса R2 = 0,4 м (рис. 2.18).
 Определить угловую скорость
Определить угловую скорость 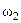 и угловое ускорение
и угловое ускорение  вала смесителя при t = 2 с, если известно, что вал двигателя вращается в соответствии с законом
вала смесителя при t = 2 с, если известно, что вал двигателя вращается в соответствии с законом  рад.
рад.
Решение. Очевидно, линейные скорости точек A и B шкивов равны (скольжением ремня и его растяжением пренебрегаем). Но  , а
, а  . Тогда
. Тогда

При указанных допущениях касательные ускорения точек A и B также равны, но
 ,
,  и тогда
и тогда
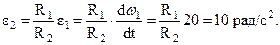
Следует заметить, что нормальные ускорения точек A и B не равны. (почему?).
Дата добавления: 2015-04-15; просмотров: 277; Мы поможем в написании вашей работы!; Нарушение авторских прав |