Определение ускорений точек тела

Запишем основное уравнение для определения скорости точки:

.

Для определения ускорения точки М вычислим векторную производную от уравнения (2.30) при этом примем во внимание, что вектор 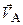изменяет только свою величину:

(2.33)

Уравнение (2.33) выражает следующую теорему.

Ускорение любой точки М при плоском движении тела равно геометрической сумме ускорений полюса от поступательного движения тела и ускорения данной точки от вращения тела вокруг полюса.

Так как определяет ускорение точки М от вращения тела вокруг полюса А, то его можно представить в виде:

(2.34)

Касательное 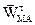и нормальное ускорения точки М от вращения тела вокруг полюса определяются на основе (2.26), (2.27):

, при этом , .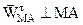

Полное ускорение находится из уравнения .

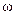Пример 2.11. Определить ускорение точки В тела, совершающего плоское движение, если известны ускорение полюса , угловая скорость , угловое ускорение и расстояние AB (рис. 2.31).

В соответствии с изложенным выше находим:

Результат представлен на рис. 2.31.

С учетом (2.34) уравнение (2.33) целесообразно записать в виде

(2.35)

В общем случае движение полюса может быть криволинейным и тогда полное ускорение произвольной точки М определяется уравнением

(2.36)