Определение абсолютного ускорения. Теорема Кориолиса

Для определения абсолютного ускорения точки при ее сложном движении необходимо вычислить векторную производную от абсолютной скорости (2.39). Примем во внимание, что вектор относительной скорости меняет свою величину и направление в относительном движении и кроме того меняет свое направление в переносном движении.

Соответственно, вектор переносной скорости меняет свою величину и направление в переносном движении, кроме того, вектор переносной скорости меняет свое направление в относительном движении.

Таким образом, производную уравнения (2.29) можно записать так:

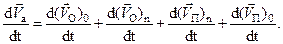
(2.41)

В уравнении (2.41) по определению

– относительное ускорение.

– переносное ускорение.

Сумма двух последних слагаемых называется ускорением Кориолиса,

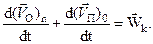
Окончательно уравнение (2.41) примем вид:

(2.42)

Уравнение (2.42) выражает следующую теорему Кориолиса:

если точка совершает сложное движение, то в общем случае ее абсолютное ускорение равно сумме трех ускорений – относительного, переносного и кориолисового.

Очевидно, ускорение Кориолиса характеризует изменение направления вектора относительна скорости в переносном движении и вектора переносного движения в относительном движении.

В рассмотренном выше примере 2.13) имеем:

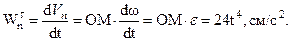
Можно доказать, что ускорение Кориолиса определяется уравнением:

(2.43)

то есть вектор ускорения Кориолиса определяется удвоенным векторным произведением вектора переносной угловой скорости 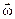и вектора относительной скорости .

Условились вектор 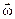направлять вдоль оси вращения в ту сторону, откуда вращение наблюдается происходящим против часовой стрелки.

Вектор ускорения Кориолиса перпендикулярен плоскости, в которой лежат векторы переносной угловой скорости и относительной скорости точки и направлен в ту сторону, откуда совмещение первого вектора со вторым происходит кратчайшим путем против часовой стрелки.

Модуль ускорения Кориолиса находится из выражения

(2.44)

В рассмотренном примере (рис. 2.34)

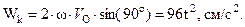
Направления векторов , , и показаны на рис. 2.36. С учетом направления этих векторов абсолютое ускорение можно вычислить по уравнению

Из анализа уравнения (2.44) следует, что ускорение Кориолиса равно нулю в двух случаях:

1) когда w = 0, т.е. когда переносное движение ПСО является поступательным;

2) когда .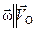

В общем случае и относительное и переносное движения могут быть криволинейными. В этом случае рабочая формула для определения абсолютного ускорения по теореме Кориолиса имеет вид:

.

(2.45)

При решении конкретных задач уравнение (2.45) необходимо спроецировать на произвольно выбранные оси координат, после чего абсолютное ускорение найдется из выражения

.

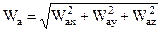(2.46)

При геометрическом решении абсолютное ускорение определяется замыкающей стороной многоугольника, построенного на основе (2.45).

Пример 2.14. Частица продукта M движется вдоль образующей центробежного конического сепаратора с постоянной скоростью 5 м/с. Определить абсолютное ускорение частицы, если ротор центрифуги вращается вокруг оси 0z с постоянной угловой скоростью 20 рад/с; принять 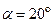; 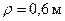(рис. 2.27).

Решение. Движение частицы M вдоль образующей будем считать относительным. Тогда переносным движением будет движение точки M по окружности переменного радиуса . Так как угловая скорость переносного вращения 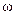и относительная скорость постоянны, то уравнение (2.45) для определения абсолютного ускорения примет вид

.

По условию задачи имеем:

;

.

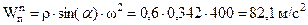Так как в данном случае 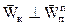, то

.

В некоторых типах центрифуг продукт движется с ускорением 1000 м/с² и выше, что обеспечивает их высокую производительность и эффективность.