Сферическое движение тела

Для удобства назовем вращение тела относительно подвижной оси OA относительным движением, а вращение вокруг неподвижной оси OB – переносным движением (рис. 2.42). Тогда величина и направление вектора абсолютной мгновенной угловой скорости будет определяться геометрической суммой векторов относительной и переносной угловых скоростей

,

(2.54)

или

Пример 2.15. В планетарном редукторе водило 1 делает 9 об/мин. Определить угловую скорость колеса 2 относительно водила; радиус неподвижного колеса 3 в 1,5 раза больше радиуса колеса 2 (рис. 2.43).

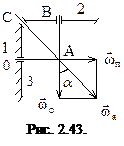Решение. Вектор относительной угловой скорости колеса 2 направлен по оси водила AB, а переносной по сои 0A. Вектор абсолютной угловой скорости должен проходить через точку C, в которой подвижное колесо 2 соприкасается с неподвижным колесом 3. Изложенное позволяет построить параллелограмм векторов угловых скоростей на основе (2.54), из которого находим .

Пусть n – число оборотов водила, тогда его угловая скорость . Угол найдем из соотношения радиусов подвижного и неподвижного колес: .

Окончательно получим:

При решении задач удобнее пользоваться аналитическим методом, спроектировав уравнение (2.54) на оси координат.

Тогда .

(2.55)

Угловое ускорение мгновенного вращения равно векторной производной от абсолютной угловой скорости по времени

	(2.56)
или	(2.57)
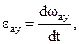
	(2.58)

Определение скоростей и ускорений точек тела при сферическом движении

Рассмотрим порядок решения таких задач применительно к произвольной точке М.

Скорость точки M можно найти как произведение абсолютной угловой скорости на расстояние точки до оси вращения

.

(2.59)

Вектор скорости точки M перпендикулярен плоскости треугольника OKM и направлен в сторону абсолютного вращения Если задать положение точки M радиусом-вектором , то вектор скорости точки M можно определить векторным произведением

.

(2.60)

Проецируя (2.60) на оси координат получим:

(2.61)

Для определения ускорения точки необходимо вычислить векторную производную от вектора скорости (2.60):

или

.

(2.62)

Первое слагаемое называется вращательным ускорением, а второе – осестремительным. Тогда

(2.63)